
PARTIE A : LE DIOXYDE DE SOUFRE ET SA SOLUTION AQUEUSE
A-1 : Donner la configuration électronique des atomes de soufre et d'oxygène
S : Z = 16 : 1s2 2s2 2p6 3s2 3p4
O : Z = 8 : 1s2 2s2 2p4
Le soufre naturel est un mélange de trois isotopes 32S, 34S et 33S. La masse molaire du mélange naturel est de de 32,06 g.mol-1
A-2 -1 : Donner la "composition" du noyau de chaque isotope.
32
S : 16 protons - 16 neutrons33
S : 16 protons - 17 neutrons34
S : 16 protons - 18 neutronsSachant que l'abondance naturelle de l'isotope 32S est de 95,1%.
A-2-2-a : évaluer approximativement l'abondance naturelle des deux autres isotopes.
M =
S xi MiMi
» Ai32,06 = 0,951*32 + 33 x+ 34y
32,06 = 30,432 + 33 x+ 34y
1,628 = 33 x + 34 y
x + y + 0,951 = 1
x + y = 0,049
y = 0,049 - x
1,628 = 33 x + 34 ( 0,049 - x )
1,628 = 33 x + 1,666 - 34 x
x = 0,038
y = 0,011
32
S : 95,1% - 33S : 3,8% - 34S : 1,1%A-2-2-b : Quelles données supplémentaires seraient nécessaires pour un calcul exact de ces abondances ?
Pour faire un calcul exact il faudrait connaître les masses molaires relatives exactes de chacun des isotopes.
Il existe également un isotope radioactif 35S
A-2-3-a : De quel type d'emetteur radiaoctif cet isotope fait-il partie ?
35
S : 16 protons et 19 neutrons par comparaison avec les isotopes stables on voit qu'il possède un "excés de neutrons", il se stabilisera en transformant 1 neutron en proton, pour cela il émetra un électron. C'est donc un émetteur de type b-.A-2-3-b : Ecrire la tranformation radioactive correspondante.

A-2 : Le dioxyde de soufre SO2
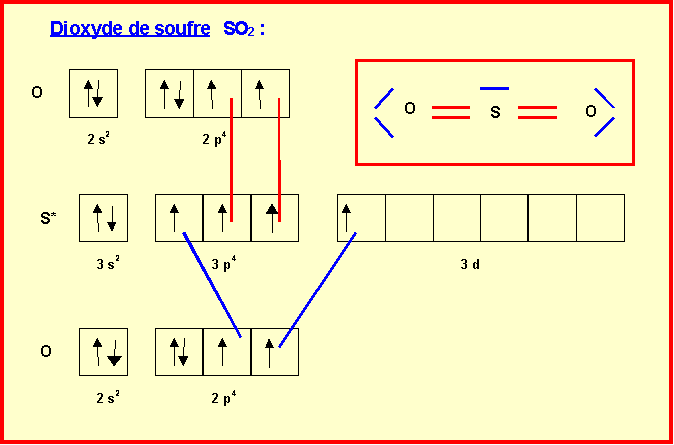
A-2-1 : Donner le schéma de Lewis de cette molécule.
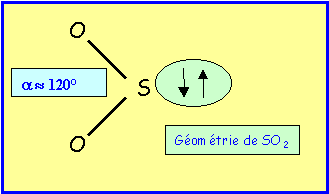
A-2-2 : En utilisant la méthode de Gillespie (V.S.E.P.R) prévoir sa géométrie et en donner une représentation spatiale.
A-2-3 : Préciser la valeur attendue pour les angles OSO.
La géométrie moléculaire autour de l'atome central S est du type AX2E.
La molécule sera donc coudée, en forme de V avec un angle proche de 120°.
L'angle OSO sera légérement inférieur à 120° à cause des répulsions doublet libre/doublet de liaison (E/X) plus importantes que les répulsions doublet de liaison/doublet de liaison (X/X). Néanmoins, la présence des deux doubles liaisons entraîne également d'assez fortes répulsions, les deux effets étant contradictoires l'angle restera très proche des 120° prévus par la V.S.E.P.R.
Remarque : La valeur expérimentale est de 119°.
A-2-4 : Que signifie le sigle V.S.E.P.R ? En donner la traduction française.
V.S.E.P.R = Valence schell électronics pairs répulsion = Répulsions des paires électroniques de la couche de valence = R.P.E.C.V
A-3 : L'ion sulfite SO32-
Dissous dans l'eau en milieu basique, le dioxyde de soufre se transforme en ion sulfite SO32-.
A-3-1 :Donner le schéma de Lewis de cet ion moléculaire.
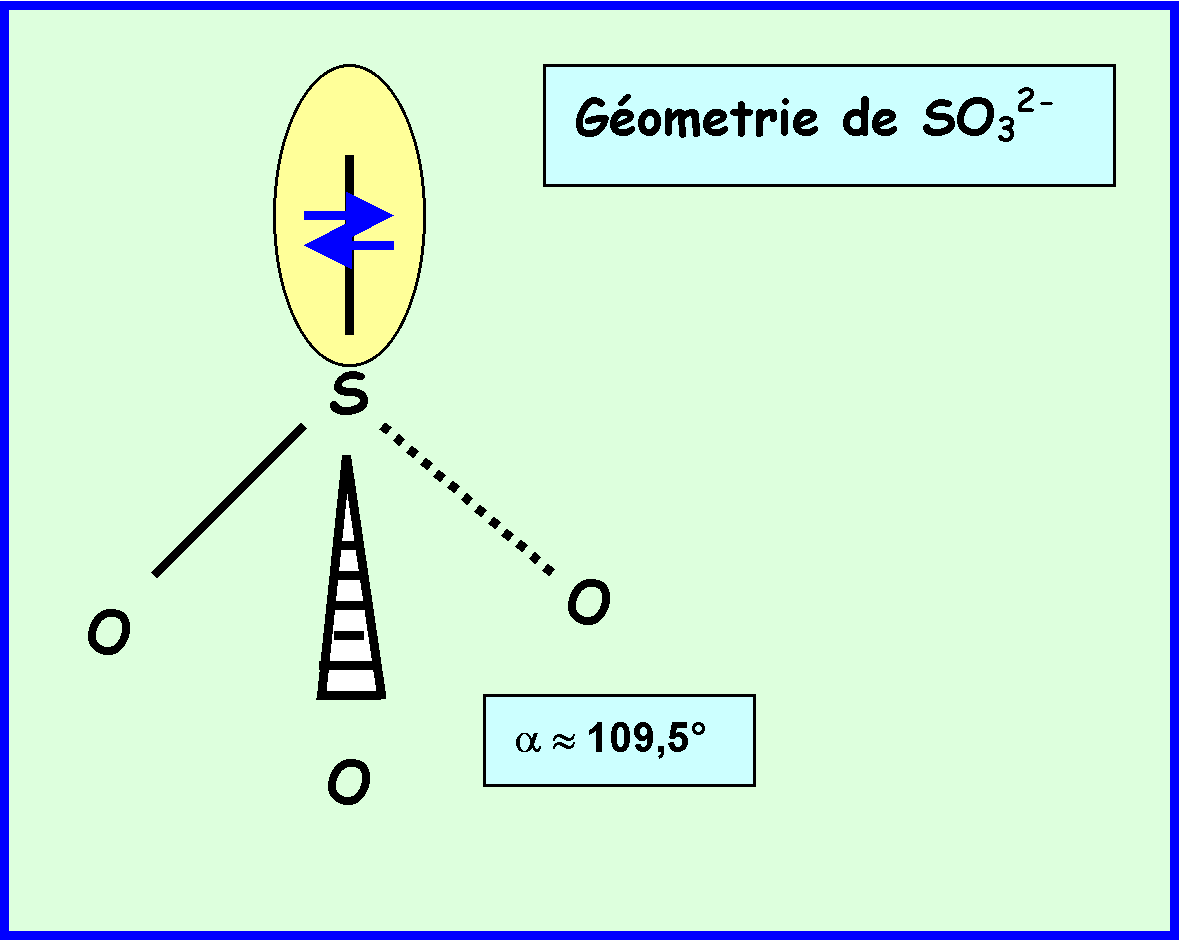
A-3-2 : En utilisant la méthode de Gillespie (V.S.E.P.R) prévoir sa géométrie et en donner une représentation spatiale.
A-3-3 : Préciser la valeur attendue pour les angles OSO.
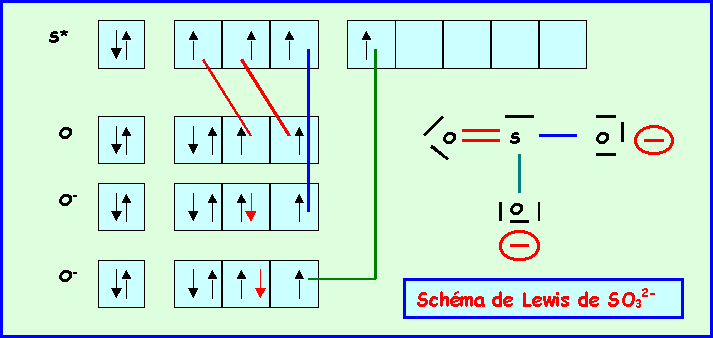
La géométrie moléculaire autour de l'atome central S est du type AX3E.
Cette géométrie correspond à un tétraèdre dont un sommet sera occupé par le doublet libre de S. (On peut aussi parler d'une géomètrie pyramidale).
L'angle OSO sera légérement inférieur à 109,5° à cause des répulsions doublet libre/doublet de liaison (E/X) plus importantes que les répulsions doublet de liaison/doublet de liaison (X/X).
A-4 : L'acide sulfureux H2SO3
Dissous dans l'eau en milieu acide, le dioxyde de soufre se transforme en acide sulfureux H2SO3.
A-3-1 :Donner le schéma de Lewis de cette molécule.
A-3-2 : En utilisant la méthode de Gillespie (V.S.E.P.R) prévoir sa géométrie et en donner une représentation spatiale.
A-3-3 : Préciser la valeur attendue pour les angles OSO et SOH.
La géométrie est du type AX2E2 autour des oxygènes et AX3E autour du soufre, tous les angles seront proches de 109,5° qui correspond au tétraèdre. Les angles SOH seront inférieurs aux angles OSO car il y a deux doublets libres au lieu d'un.
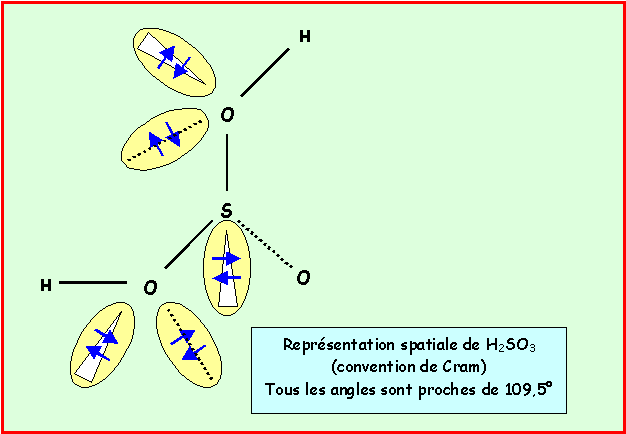
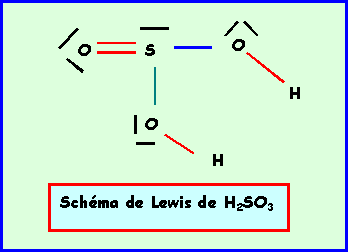
A-4 : La solution aqueuse de H2SO3
L'acide sulfureux est un diacide dont les valeurs de pKa sont : pK1=1,8 et pK2=7,2
A-4-1 : Ecrire les deux réactions et définir les deux constantes d'acidité K1 et K2
H2SO3(aq) + H2O = HSO3-(aq) + H3O+ (aq) : K1 = [HSO3-] [H3O+] / [H2SO3]
HSO3-(aq) + H2O = SO32-(aq) + H3O+ (aq) : K2 = [SO32-] [H3O+] / [HSO3-]
A-4-2 : Ecrire les diverses relations qui permettent de calculer le pH d'une solution aqueuse de H2SO3 de concentration C mol.L-1.
K1 = [HSO3-] [H3O+] / [H2SO3]
K2 = [SO32-] [H3O+] / [HSO3-]
Ke = [H3O+] [OH-]
Conservation de la matière :
[H2SO3] + [HSO3-] + [SO32-] = C
Electroneutralité de la solution :
[HSO3-] + 2 [SO32-] + [OH-] = [H3O+]
Le calcul du pH est possible sans faire aucune approximation mais pour simplifier le problème les chimistes ont pris l'habitude de faire quelques approximations raisonnables.
La première approximation classique dans ce type de problème est de ne tenir compte que de la première acidité de H2SO3 et donc de négliger la seconde.
A-4-3 : Dans le cadre de cette approximation classique montrer les simplifications qui en découlent dans les diverses équations établies précédemment.
Si on néglige la deuxième réaction on aura :
K1 = [HSO3-] [H3O+] / [H2SO3]
Ke = [H3O+] [OH-]
Conservation de la matière :
[H2SO3] + [HSO3-] = C
Eléctroneutralité de la solution :
[HSO3-] + [OH-] = [H3O+]
A-4-4: Le problème restant relativement complexe, on cherche à le simplifier à nouveau. Pour cela on suppose que la solution est suffisamment acide pour pouvoir négliger la présence d'ion hydroxyde. Que deviennent alors les équations précédentes ?
Si on néglige la présence d'ion OH-, on a :
K1 = [HSO3-] [H3O+] / [H2SO3]
[H2SO3] + [HSO3-] = C
[HSO3-] = [H3O+]
A-4-5 : Résoudre le problème dans ce cadre et calculer le pH de la solution pour C=0,01 mol.L-1.
K1 = [HSO3-] [H3O+] / [H2SO3]
[HSO3-] = [H3O+] = h
[H2SO3] = C - [HSO3-] = C - h
K1 = h2 / (C - h )
K1 (C - h ) = h2
K1 C - K1 h = h2
h2 + K1 h - K1 C
D
= K12 + 4 K1 Ch = 1/2 { - K1 +
Ö ( K12 + 4 K1 C) }A.N : h = 0,00695124 et pH = -log h = 2,16
A-4-6 : Calculer ensuite pour le pH trouvé les concentrations de toutes les espèces présentes en solution et vérifier ainsi la validité des deux aproximations faites.
On a :
h = 0,00695
[OH-] = 10-14/ h = 1,44 10-12 mol.L-1.
On pouvait donc bien négliger la présence de OH-.
On a donc bien : h = [HSO3-] = 0,00695 mol.L-1.
K1 = [HSO3-] [H3O+] / [H2SO3]
[H2SO3]= [HSO3-] [H3O+] / K1 = h2 / K1 = 0,0305 mol.L-1
K2 = [SO32-] [H3O+] / [HSO3-]
[SO32-] = K2 [HSO3-] / [H3O+] = K2 = 10-7,2
La présence de SO32- est bien négligeable et on peut donc bien ne pas tenir compte de la deuxième acidité.
A-4-7 : On aurait pu simplifier encore plus le problème en supposant que la première acidité de H2SO3 est suffisamment faible pour que l'on puisse négliger sa dissociation.
Quelle formule classique obtient-on dans ce cadre ? Cette formule simplifiée est-elle valable dans le cas qui nous interesse si on veut pH à 0,1 unité près ?
K1 = h2 / C
h2 = K1C
pH = 1/2 ( pK1 - log C )
pH = 0,5 (1,8 + 2 ) = 1,9
Cette valeur est incorrecte à 0,1 unité de pH près. On doit tenir compte de la dissociation non négligeable de H2SO3.
A-9 : Titrage de l'acide sulfureux par la soude
La courbe de titrage pH-métrique de 20 mL d'une solution de H2SO3 de molarité inconnue par de la soude à 0,1 mol.L-1 vous est fournie en annexe.
A-9-1 : Quelle est la molarité de H2SO3 ?
On peut utiliser soit le premier point équivalent soit le deuxième.
Avec P.E.1 :
La réaction de titrage est :
H2SO3 + OH- = HSO3- + H2O
On a : Ca Va = Cb Vb
Ca = Cb Vb / Va
Cb=0,1 mol.L-1
Vbe1 = 8 mL (voir courbe)
Va = 20 mL
Ca = 8 * 0,1/ 20 = 0,04 mol.L-1
Avec P.E.2 :
La réaction de titrage est :
H2SO3 + 2 OH- = SO32- + 2 H2O
On a : 2 Ca Va = Cb Vb
Ca = Cb Vb / 2 Va
Cb=0,1 mol.L-1
Vbe1 = 16 mL (voir courbe)
Va = 20 mL
Ca = 16 * 0,1/ 40 = 0,04 mol.L-1
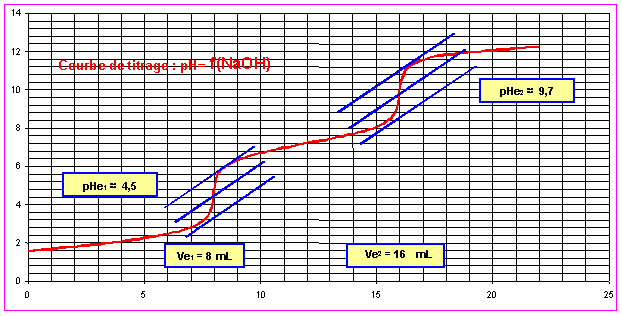
A-9-2 : Quel est le pH au premier point équivalent ?
Etablir la relation qui permet de le calculer et vérifier l'accord avec la courbe fournie.
Au premier point équivalent on est en présence d'une solution de l'ampholyte HSO3- le pH est donné approximativement par :
pH = 1/2 ( pK1 + pK2 ) = = 1/2 ( 1,8 + 7,2 ) = 4,5.
Sur la courbe on trouve bien un pH proche de cette valeur. Il est en pratique difficile d'apprécier précisement ce pH en raison de la forte variation de celui-ci au environ du point équivalent. La méthode des tangentes ne permet que de l'évaluer approximativement mais pas avec une grande précision.
Etablissement de la formule approchée
:Solution de NaHSO3
Relations entre les inconnues
(1) C.M (SO3) : [HSO3-] + [SO32-] + [H2SO3] = C
(2) E.N : [HSO3-] + 2 [SO32-] + [OH-] = [H3O+] + [Na+]
(3) C.M (Na) : [Na+] = C
(4) K1 = [HSO3-] [H3O+] / [H2SO3]
(5) K2 = [SO32-] [H3O+] / [HSO3-]
(6) Ke = [H3O+] [OH-]
On peut donc résoudre exactement le problème sans approximations.
On peut aussi le simplifier par des approximations raisonnables.
Ici on a affaire a une solution d'ampholyte, on peut faire l'hypothèse que le pH ne sera ni très acide ni très basique. On pourra donc a priori négliger les concentrations de H3O+ et OH- devant C=[Na+] dans l'équation d'électroneutralité.
(2') E.N : [HSO3-] + 2 [SO32-] = C
(1) C.M (SO3) : [HSO3-] + [SO32-] + [H2SO3] = C
Par différence (2')-(1) on trouve :
[SO32-] = [H2SO3]
En faisant le produit de K1 par K2 on trouve :
K1 K2 = { [HSO3-] [H3O+] / [H2SO3] } { [SO32-] [H3O+] / [HSO3-] } = [H3O+]2
Soit pH = 1/2 (pK1+pK2)
Avec pH = 4,5 soit [H3O+] = 10-4,5 et [OH-] = 10-9,5 et C = 0,04*20/28 = 0,0286 mol.L-1 l'approximation semble légitime.
Un calcul sans approximation conduit à pH = 4,59 on est donc à 0,1 unité de pH près ce qui est tout de même limite.
A-9-3 : Quel est le pH au deuxième point équivalent ?
Etablir la relation qui permet de le calculer et vérifier l'accord avec la courbe fournie.
A la deuxième équivalence on est en présence d'une solution de SO32-.
Si on fait l'hypothèse de négliger sa deuxième basicité devant la première on arrive à l'aproximation classique :
pH = 7 + 1/2 pK2 + 1/2 log C
Avec C = 0,04*20/36 = 0,0222 on obtient pH = 9,77.
Sur la courbe on lit bien un pH proche de cette valeur.
Comme précédement, il est difficile d'apprécier précisement ce pH en raison de la forte variation de celui-ci au environ du point équivalent. La méthode des tangentes permet de l'évaluer approximativement mais pas avec une grande précision.
Etablissement de la formule approchée
:Solution de Na2SO3
Relations entre les inconnues
(1) C.M (SO3) : [HSO3-] + [SO32-] + [H2SO3] = C
(2) E.N : [HSO3-] + 2 [SO32-] + [OH-] = [H3O+] + [Na+]
(3) C.M (Na) : [Na+] = 2 C
(4) Kb1 = [HSO3-] [OH-] / [SO32-]
(5) Kb2 = [H2SO3] [OH-] / [HSO3-]
(6) Ke = [H3O+] [OH-]
On peut donc résoudre exactement le problème sans approximations.
On peut aussi le simplifier par des approximations raisonnables.
Ici on a affaire a une solution de SO32- dibase, on peut faire l'hypothèse que le pH sera franchement basique. On pourra donc a priori négliger les concentrations de H3O+ devant celle de OH- et devant 2 C=[Na+] dans l'équation d'électroneutralité.
(2') E.N : [HSO3-] + 2 [SO32-] + [OH-] = 2 C
On peut faire l'hypothèse supplémentaire de considérer le pH suffisemment basique pour que la concentration de H2SO3 soit négligeable, ce qui revient bien à négliger la deuxième basicité de SO32-.
(1') C.M (SO3) : [HSO3-] + [SO32-] = C ou [SO32-] = C - [HSO3-]
(2') devient [SO32-] = C - [OH-]
On a donc : [HSO3-] = [OH-]
Kb1 = [HSO3-] [OH-] / [SO32-]
Kb1 = [ [OH-]2 / (C - [HSO3-] )
Kb1 = [ [OH-]2 / (C - [OH-] )
Kb1 = w2/(C-w)
On peut résoudre cette équation du second degré.
On peut simplifier encore le problème en négligeant [OH-] devant C.
On obtient alors Kb1 C = [OH-]2
Soit pOH = 1/2 ( pKb1 - log C )
Soit pH = 14 - 1/2 pKb1 + 1/2 log C
pH = 14 - 1/2 ( 14 - pK2 ) + 1/2 log C
pH = 7 + pK2 + 1/2 log C = 9,77
Une résolution sans approximation conduit à la même valeur de pH.
L'approximation est donc excellente.
PARTIE B : ETUDE D'UN TITRAGE
On réalise le titrage de Va mL d'une solution aqueuse de A de molarité Ca par une solution aqueuse de B de molarité Cb.
La réaction de titrage est la suivante : 2 A(aq) + 3 B(aq) = A2B3(s)
La détermination du point équivalent du titrage se fait par utilisation d'un indicateur coloré bien choisi. On donne log KR = 30 pour cette réaction.
On suppose que l'on verse progressivement la solution de B dans la solution de A.
B-1: Donner un schéma légendé du montage utilisé en pratique pour ce titrage.
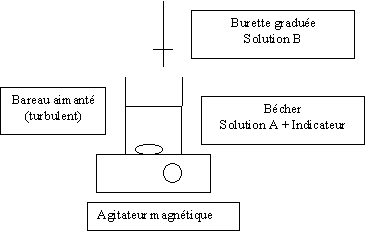
B-2 : Décrire un protocole opératoire clair en précisant bien le matériel utilisé.
Dans un bécher introduire Va = 20 mL (mesurés à la pipette) de solution A et quelques gouttes d'indicateur coloré.
Introduire un bareau aimanté et poser sur un agitateur magnétique.
Remplir une burette graduée avec la solution B. Ajuster au zéro.
Verser progressivement la solution B dans le bécher sous agitation. Arréter le titrage au changement de teinte de l'indicateur. Noter le volume Vb versé pour atteindre le Point Equivalent.
B-3 : Etablir les relations qui permettent de tracer la courbe de titrage :
pA = -log [A] = f(Vb)
On pourra pour simplifier le problème faire une (des) approximation(s) que l'on justifiera.
2 A(aq) + 3 B(aq) = A2B3(s)
Détermination du Point equivalent :
3 Ca Va = 2 Cb Vb
Vb Eq = 3 Ca Va / 2 Cb = 3*20*0,015/ (2*0,025) = 18 mL
La constante de réaction étant très élevée, on peut faire l'approximation de considérer la réaction comme totale.
Avant le point équivalent
: 0 < Vb < 18 mL
2 A(aq) + 3 B(aq) = A2B3(s)
A est en excès et B en défaut
|
A(aq) |
B(aq) |
|
|
Etat initial |
Ca Va (Excès) |
Cb Vb (défaut) |
|
Etat final |
CaVa - 2/3 Cb Vb |
0 |
[A] = { ( CaVa - 2/3 Cb Vb ) / (Va + Vb) }
pA = -log { ( CaVa - 2/3 Cb Vb ) / (Va + Vb) }
Près le point équivalent
: Vb > 18 mL
2 A(aq) + 3 B(aq) = A2B3(s)
A est en défaut et B en excès
|
A(aq) |
B(aq) |
|
|
Etat initial |
Ca Va (défaut) |
Cb Vb(Excès) |
|
Etat final |
0 |
CbVb - 3/2 Ca Va |
[B] = { ( CbVb - 3/2 Ca Va ) / (Va + Vb) }
KR = 1 / { [A]2 [B]3 }
Log KR = - log { [A]2 [B]3 }
Log KR = - 2 log [A] - 3 log [B]
- 2 log [A] = Log KR + 3 log [B]
pA = 1/2 Log KR + 3/2 log [B]
pA = 1/2 Log KR + 3/2 log { ( CbVb - 3/2 Ca Va ) / (Va + Vb) }
Au point équivalent : Vb = 18 mL
2 A(aq) + 3 B(aq) = A2B3(s)
On est dans les proportions stoéchiométriques.
|
A(aq) |
B(aq) |
|
|
Etat initial |
Ca Va |
Cb Vb |
|
Etat final |
2 e |
3 e |
[A] = 2
e / (Va + Vb)[B] = 3
e / (Va + Vb)
KR = 1 / { [A]2 [B]3 }
KR = (Va + Vb )5 / { [2
e]2 [3 e]3 }
B-4 : Tracer cette courbe pour Ca=0,015 mol.L-1 Va = 20 mL et Cb=0,025 mol.L-1
Avant le point équivalent
: Vb < 18 mLpA = -log { ( CaVa - 2/3 Cb Vb ) / (Va + Vb) }
pA = -log { ( 0,3 - 2/3 0,025 Vb ) / (20 + Vb) }
pA = -log { ( 0,3 - 0,0167 Vb ) / (20 + Vb) }
Après le point équivalent
: Vb > 18 mLpA = 1/2 Log KR + 3/2 log { ( CbVb - 3/2 Ca Va ) / (Va + Vb) }
pA = 15 + 3/2 log { ( 0,025 Vb - 0,45 ) / (20 + Vb) }
Au point équivalent
: Vb = 18 mLKR = (Va + Vb )5 / { [2
e]2 [3 e]3 }KR = (38 10-3 )5 / { [2
e]2 [3 e]3 }1030 = 7,9235 10-8 / ( 108
e5 )108 e5 = 7,9235 10-38
e
5 = 7,9235 10-38 / 108 = 7,336 10-40e
= 1,49 10-8 mole[A] = 2
e / (Va + Vb)[A] = 2
* 1,49 10-8 / 38 10-3 = 7,84 10-7pA = 6,105
|
Vb |
pA |
Vb |
pA |
|
2 |
1,92 |
18,1 |
8,73 |
|
4 |
2,01 |
18,2 |
9,18 |
|
6 |
2,11 |
18,5 |
9,77 |
|
8 |
2,23 |
19 |
10,21 |
|
10 |
2,35 |
20 |
10,65 |
|
12 |
2,51 |
22 |
11,07 |
|
14 |
2,71 |
24 |
11,30 |
|
16 |
3,04 |
26 |
11,46 |
|
17 |
3,36 |
28 |
11,58 |
|
17,5 |
3,68 |
30 |
11,67 |
|
17,8 |
4,14 |
32 |
11,74 |
|
17,9 |
4,55 |
34 |
11,80 |
|
18 |
6,11 |
36 |
11,86 |
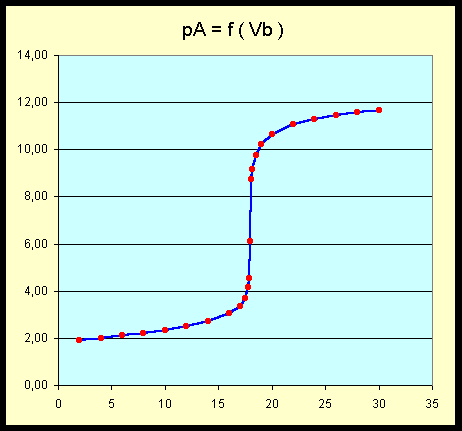
B-5 : A quelle condition doit satisfaire l'indicateur pour pouvoir être utilisé pour ce titrage.
Son changement de couleur doit se produire pour un pA proche de 6,1.
Dans la pratique pour 4,6 < pA < 8,7 pour que son virage corresponde au point équivalent à 0,1 mL près.