UNIVERSITE DE LA REUNION ANNEE UNIVERSITAIRE 1997-1998
FACULTE DES SCIENCES SESSION DE SEPTEMBRE 98
CHIMIE THEORIQUE-ATOMISTIQUE
THERMODYNAMIQUE
DEUXIEME PERIODE
Formulaire - Rappels - Données :
On rappelle la formule permettant le calcul approché du rayon de covalence d’un atome: R(A°) = 0,215 n2/Z* + 0,148 n + 0,225
Z*O = 4,55 Z*S = 5,45 (Pour H on prendra la valeur RH = 0,346 A°)
On rappelle la formule permettant le calcul approché des longueurs de liaisons.
L(A°) = 1,11 Lcalc - 0,203 (Lcalc = longueur calculée par addition des rayons de covalence)
Double liaison = 86 % de la simple - Triple liaison = 78 % de la simple
On rappelle la formule empirique de Hanney-Smith permettant le calcul du pourcentage ionique d’une liaison à partir de l’écart d’électronégativité Dx :
%ion = 16 (Dx )+ 3,5 (Dx)2
Echelle d’électronégativité de Pauling : (DX)2 = EAB - Ö ( EAA * EBB )
Energies de liaisons en k J mol-1 :
EH-H = 436 ; ES-H = 368 ; ES-S = 266 ; EO-H = 463 ; EO-O = 143
1 D = 3,33 10-30 C.m 1 F = 96500 C e = 1,6 10-19 C 1A° = 10-10 m
H2S est un diacide faible pK1 = 7 et pK2 = 13
Exercice 1 : Composés Hydrogénés de l’Oxygène et du Soufre
1) Quels sont les composés hydrogénés prévisibles pour ces deux éléments ?
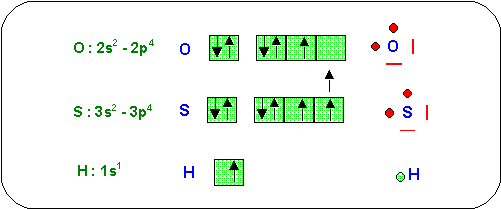
Les formules se déduisent des schémas de Lewis des atomes concernés.

O et S sont divalents (2 électrons célibataires) et H est monovalent (1 électron célibataire). Il faut donc associer deux atomes d'Hydrogène à 1 atome de Soufre ou d'Oxygène. Les composés hydrogénés les plus probables sont donc H2O et H2S.
2) Donner une structure de Lewis des molécules correspondantes.
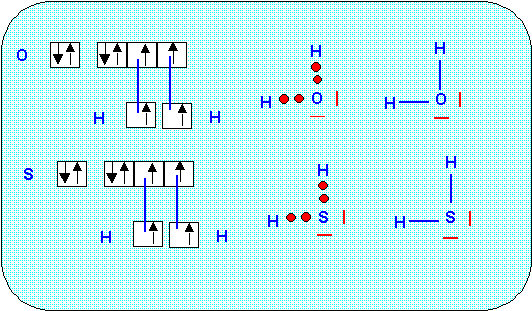
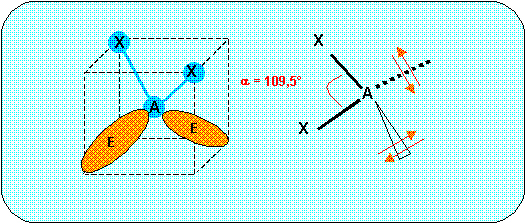
3) Quelle est la géométrie prévisible de ces molécules. On fera un dessin représentant les molécules dans l’espace et on précisera les angles prévus théoriquement.
Ces deux molécules sont du type AX2E2, la figure de répulsion correspondante est le tétraèdre. Deux des sommets sont occupés par les deux doublets libres, la molécule aura la forme d'un V avec un angle proche de 109,5 °.
4) Les données expérimentales concernant ces molécules sont les suivantes :
ATTENTION : LES VALEURS SONT DONNEES DANS LE DESORDRE
Longueur de Liaison : 0,96 A° et 1,35 A°
Angles HXH : 92 ° et 105 °
Moments Dipolaires des molécules : 0,95 D et 1,85 D

Entre S et O, quel est l’élément le plus électronégatif ?
O et S appartiennent à la même colonne, O est situé au-dessus de S.
O est donc plus électronégatif que S : XO > XS
b) Déterminer quantitativement les électronégativités de O et S dans l’échelle de Pauling. On prendra comme référence XH = 2,2.
Echelle d’électronégativité de Pauling : (DX)2 = EAB - Ö ( EAA * EBB )
Les énergies de liaisons doivent être exprimées en eV par atome.
Pour convertir les Kj mol-1 en eV / atome on multiplie par 1000 pour passer aux joules mol-1, puis on divise par e (charge élémentaire) pour passer aux eV mol-1 puis on divise par N (nombre d'Avogadro) pour passer aux eV/atome.
Kj mol-1 * 1000 / Ne à eV / atome
Le produit N * e équivalent à la charge d'une mole d'électrons, est appelé le Faraday (F) et vaut 96500 C.
Kj mol-1 * 1000/96500 à eV/atome
Kj mol-1 * 1 / 96,5 à eV/atome
Il suffit donc de diviser l'énergie en KJ mol-1 par 96,5 pour obtenir l'énergie en eV/atome.
| H - H | S - H | O - H | O - O | S - S | |
| En KJ mol-1 | 436 | 368 | 463 | 143 | 266 |
| En eV/atome | 4,52 | 3,81 | 4,80 | 1,48 | 2,76 |
Détermination de XO :
(DXOH)2 = EOH - Ö ( EOO * EHH )
(DXOH)2 = 4,80 - Ö ( 1,48 * 4,52 ) = 2,21
DXOH = 1,49
Deux solutions sont a priori possibles :
Soit O est plus électronégatif que H à XO > XH è DXOH = XO -XHà XO = DXOH + XH = 3,69
Soit H est plus électronégatif que O à XH > XO è DXOH = XH -XOà XO = XH - DXOH = 0,72
On sait que l'eau se dissocie partiellement en H+ et OH-, cela montre que O est plus électronégatif que H (sinon on obtiendrait H- et OH+) on a donc : XO = DXOH + XH = 3,69
Détermination de XS :
(DXHS)2 = EHS - Ö ( ESS * EHH )
(DXHS)2 = 3,81 - Ö ( 2,76 * 4,52 ) = 0,28
DXSH = 0,53
Deux solutions sont a priori possibles :
Soit S est plus électronégatif que H à XS > XH è DXSH = XS -XHà XS = DXSH + XH = 2,73
Soit H est plus électronégatif que S à XH > XS è DXSH = XH -XSà XS = XH - DXSH = 1,67
On sait que H2S se dissocie partiellement en H+ ,SH- et S2- (diacide faible), cela montre que S est plus électronégatif que H (sinon on obtiendrait H-, SH+ et S2+) on a donc :
XS = DXSH + XH = 1,67
Remarque : on retrouve bien que XO > XS
c) Compte tenu des électronégativités différentes de O et S et de la présence éventuelle de doublets libres comment vont être modifiés les angles HXH ?
Attribuer à chaque molécule la valeur réelle de cet angle.
Effet des doublets libres :
Ceux-ci sont, en moyenne, plus près de l'atome central que les doublets de liaison et exercent donc de plus fortes répulsions.
Ces répulsions sont dans l'ordre décroissant : REE > REX > RXX
En conséquence l'angle XAX va être sensiblement diminué.

Influence de la nature de l'atome central :
La nature de l'atome central influence la géométrie moléculaire.
C'est essentiellement l'électronégativité qui va être à l'origine des modifications des angles entre liaisons.
Plus un atome est électronégatif et plus il attire fortement les électrons. Les doublets de liaisons seront donc d'autant plus près de l'atome central que celui-ci sera fortement électronégatif.
Si les doublets sont plus près les uns des autres ils exerceront des répulsions plus importantes entre eux, ce qui aura tendance a augmenter l'angle correspondant.
Dans le cas qui nous intéresse l'angle HOH sera plus élevé que l'angle HSH puisque O est plus électronégatif que S.
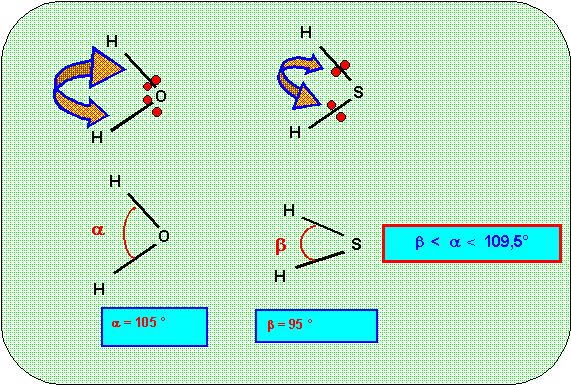
d) Pour les liaisons O - H et S - H . Calculer en utilisant les formules rappelées plus haut :
* Le pourcentage ionique des liaisons.
Formule empirique de Hanney-Smith : %ion = 16 (Dx )+ 3,5 (Dx)2
Liaison SH : DXSH = 0,53 è %ion = 9,5 %
Liaison OH : DXOH = 1,49 è %ion = 31,6 %
L(A°) = 1,11 Lcalc - 0,203
(Lcalc = longueur calculée par addition des rayons de covalence)
R(A°) = 0,215 n2/Z* + 0,148 n + 0,225 (Pour H on prendra la valeur RH = 0,346 A°)
Z*O = 4,55 Z*S = 5,45
RO = 0,215*4/4,55 + 0,148*2 +0,225 = 0,71 A°
RS = 0,215*9/5,45 + 0,148*3 +0,225 = 1,024 A°
dOH = 1,11 * (0,346 + 0,71) - 0,203 = 0,97 A° au lieu de 0,96 A° soit 1% d'écart.
dSH = 1,11 * (0,346 + 1,024) - 0,203 =1,32 A° au lieu de 1,35 A° soit 2,2 % d'écart.
* Le moment dipolaire de liaison.
m = d * d
Calcul de d :
%ion = 100 * d / e è d = %ion * e / 100
Liaison OH :
d = 31,6 * 1,6 10-19 / 100 = 5,056 10-20 C
Liaison SH :
d = 9,5 * 1,6 10-19 / 100 = 1,52 10-20 C
Calcul de m :
Liaison OH :
a) A partir des valeurs calculées : m= 5,056 10-20 * 0,96 10-10 = 4,853 10-30 C m
soit 4,853 10-30 / 3,33 10-30 = 1,46 D
b) A partir des valeurs expérimentales : m= 5,056 10-20 * 0,97 10-10 = 4,904 10-30 C m
soit 4,853 10-30 / 3,33 10-30 = 1,47 D
Liaison SH :
a) A partir des valeurs calculées : m= 1,52 10-20 * 1,32 10-10 = 2,006 10-30 C m
soit 2,006 10-30 / 3,33 10-30 = 0,602 D
b) A partir des valeurs expérimentales : m= 1,52 10-20 * 1,35 10-10 = 2,052 10-30 C m
soit 2,052 10-30 / 3,33 10-30 = 0,616 D
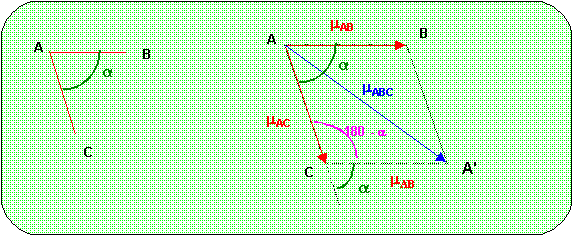
Théorème de Pythagore généralisé : Triangle ACA'
mABC2 = mAB2 + mAC2 - 2 mAB mAC cos (180 - a)
mABC2 = mAB2 + mAC2 + 2 mAB mAC cos a
Molécule H2S :
mAB = mAC = mSH = 0,602 D (ou 0,616 D) et a = 95 °
mH2S2 = mSH2 + mSH2 + 2 mSH mSH cos a
mH2S2 = 2 mSH2 (1+ cos a) = 2 * 0,6022 * (1 + cos 95) = 0,662 (ou 0,693)
mH2S = 0,813 D (ou 0,832 D)
Cette valeur est à rapprocher de la valeur expérimentale de 0,95 D soit un écart de 14,4 % (ou 12,4 %). Cet écart relativement important est du essentiellement à l'imprécision de la formule empirique de Haney-Smith qui ne permet d'obtenir qu'un ordre de grandeur pour le pourcentage d'ionicité de la liaison. Cet écart est toutefois raisonnable compte tenu de la simplicité de la formule utilisée.
Molécule H2O :
mAB = mAC = mOH = 1,46 D (ou 1,47 D) et a = 105 °
mH2O2 = mOH2 + mOH2 + 2 mOH mOH cos a
mH2O2 = 2 mOH2 (1+ cos a) = 2 * 1,462 * (1 + cos 105) = 3,16 (ou 3,203)
mH2O = 1,78 D (ou 1,79 D)
Cette valeur est à rapprocher de la valeur expérimentale de 1,85 D soit un écart de 3,7 % (ou 3,2 %). Cet écart relativement peu important est du essentiellement à l'imprécision de la formule empirique de Haney-Smith qui ne permet d'obtenir qu'un ordre de grandeur pour le pourcentage d'ionicité de la liaison. Cet écart est toutefois très raisonnable compte tenu de la simplicité de la formule utilisée.
Exercice 2 :
Pour les molécules ou ions suivants : ICl3 - N2F4 - HCN - PO43-
ICl3
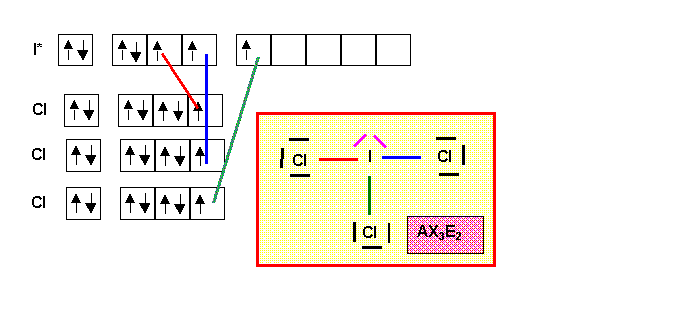
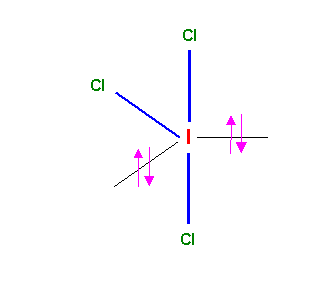
La géométrie de la molécule du type AX3E2 est basée sur la bi-pyramide à base triangulaire. Deux des sommets équatoriaux sont occupés par les doublets libres plus "encombrants" que les doublets de liaisons. On obtient une molécule en forme de T avec des angles Cl-I-Cl de 90°. La structure de Lewis obtenue ne présente pas de mésomérie particulière. La géométrie de l'atome central AX3E2 correspond à une hybridation de type sp3d.
N2F4

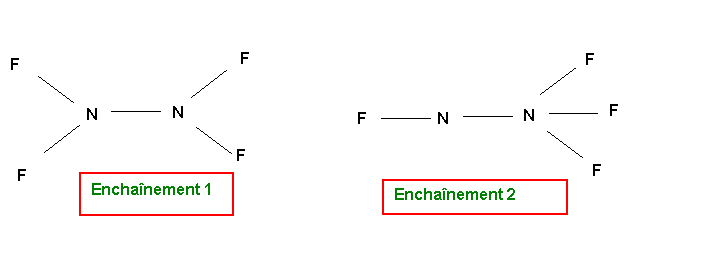
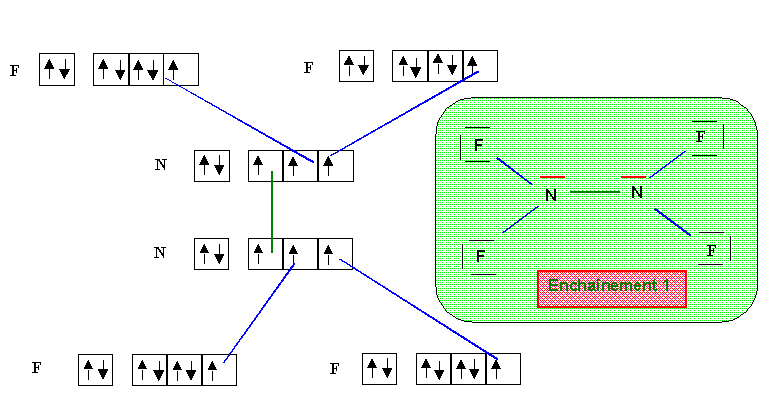
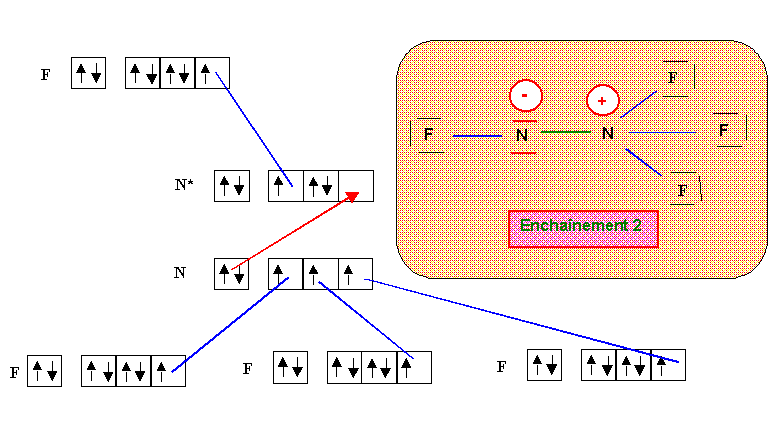
Parmis ces deux formes qui ne sont pas mésomères mais isomères, la forme 1 paraît de loin la plus probable (symetrie de la molécule et absence de charges). Au point de vue géométrique, tous les atomes d'azote sont de type tétraédrique (AX3E, AX2E2 ou AX4) et donc l'hybridation est du type sp3 dans tous les cas avec des angles proches de 109,5°. Dans les deux formes 1 ou 2 tous les atomes d'azote ou de fluor présente le maximum de liaisons qui leur soit possible de faire compte tenu de leur nombre respectif de doublets libres (pour rappel, ce nombre maximal de liaison est égal au nombre de cases quantiques de la couche de valence moins le nombre de doublets libres de l'atome concerné). La mésomèrie consistant à déplacer un doublet libre ou un doublet de liaison multiple implique qu'un des atomes voit son nombre de liaisons augmenter. Cela n'est pas possible ici et il est donc inutile de chercher des formes mésomères suplémentaires pour les formes 1 ou 2.
HCN
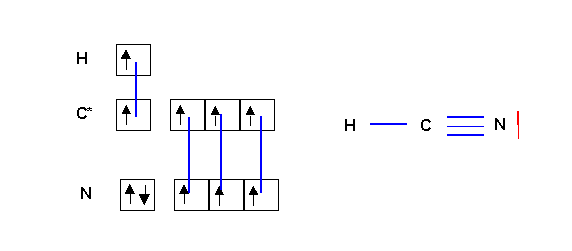
Cette forme respecte la règle de l'octet pour C et N et ne présente pas de charge formelles et sera donc la forme mésomère très largement majoritaire. Mais il n'est pas impossible d'obtenir une deuxième forme chargée et de poids statistique très faible par déplacement d'un des doublets de la triple liaison. Cette forme est toutefois extrêmement peu représentative puisqu'elle ne respecte pas la différence d'électronégativité entre C et N ( XN > XC ). On pourra donc la négliger totalement oui presque.
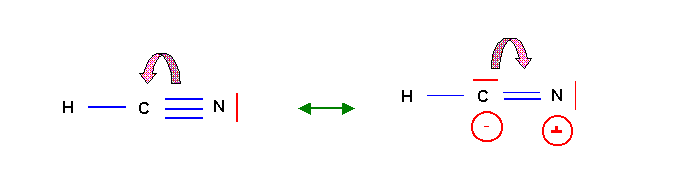
Pour ce convaincre qu'une telle forme est tout de même possible on peut construire son schéma de Lewis par la méthode classique.
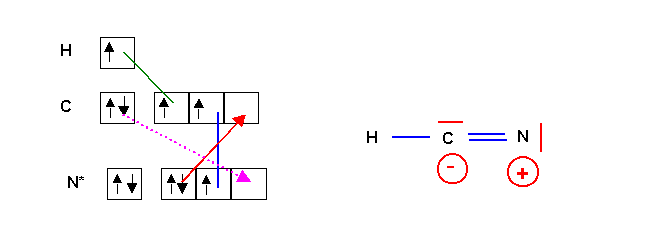
La liaison dative en pointillé rose permet de réobtenir directement la forme principale. Comme le nombre de liaisons doit être maximal cette liaison se créera "spontanément" et la forme 1 sera donc la seule à exister pratiquement. La forme 2 très "exotique" aura un poids statistique quasiment nul.
Au point de vue géométrique la forme principale est linéaire type AX2 avec une hybridation sp pour le carbone. (La forme 2 serait de type AX2E avec une hybridation sp2.)
PO43-
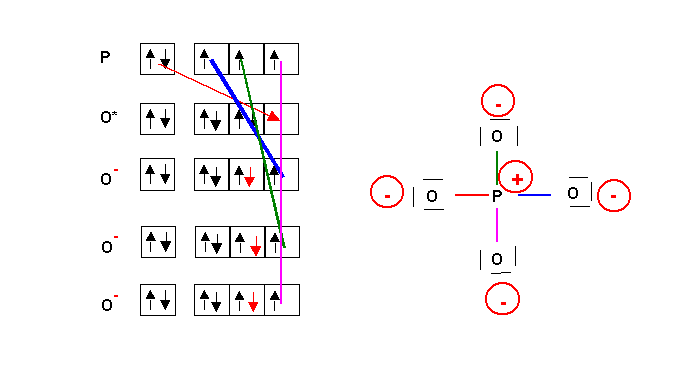
Cette forme mésomère n'est pas la plus représentative, elle présente trop de charges. On peut obtenir une meilleure forme par déplacement de doublets :
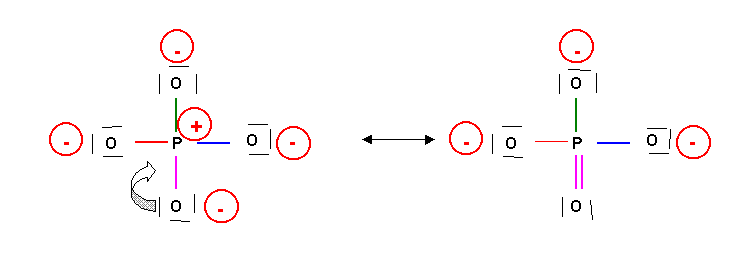
Cette nouvelle forme limite existe elle même sous 4 formes en échangeant le rôle des oxygènes. On pourrait même écrire des formes supplémentaires de poids statistique plus faible en faisant intervenir d'avantage de doubles liaisons. En résumé il existe de multiples formes mésomères et on peut représenter la molécule réelle de la façon suivante :
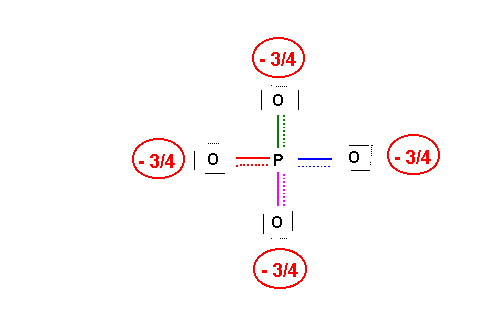
La géométrie est tétraédrique de type AX4 et l'hybridation du Phosphore central est du type sp3 (les doubles liaisons impliquent alors des orbitales d)
Exercice 1 : Mélanges binaires
On étudie la solidification de mélanges liquides AB de compositions différentes. On obtient les résultats suivants :
| xA | 0 |
0,1 |
0,2 |
0,322 |
0,44 |
0,5 |
0,6 |
0,7 |
0,8 |
0,9 |
1 |
| Tsolid | 210 |
190 |
170 |
128 |
80 |
150 |
204 |
248 |
290 |
330 |
355 |
Et on trace le graphique correspondant :
xA : fraction molaire de A dans le mélange
Tsolid : Température de solidification du mélange liquide
T fus A = 355 °C
T fus B = 210 °C
Eutectique : Mélange se comportant comme un corps pur (température de changement d'état constante), les deux phases en présence ont la même composition chimique.
3) Donner la température de fusion et la composition de l'eutectique du mélange AB qu'on peut déduire des points expérimentaux.
T fus E = 80 °C
xA = 0,44
4) Compléter le diagramme en faisant apparaître les divers domaines pour lesquels on précisera la nature des phases en présence.
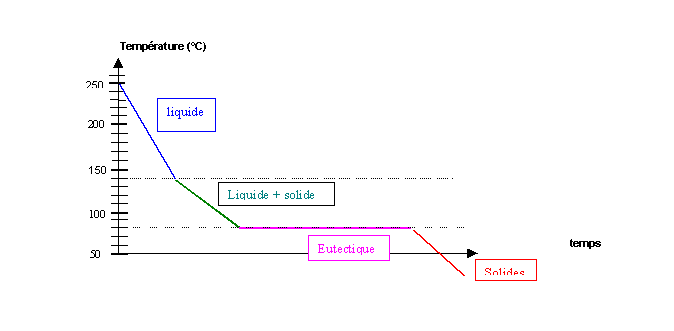
Composition du solide : B pur (Point S)
Composition du liquide : xA = 0,36 et xB = 0,64 (Point L)
Est-il possible de déterminer la composition de ce mélange ? NON
- Si non, quelles sont les compositions possibles ? Comment lever l'indétermination ?
Pour T = 110 °C deux compositions sont possibles pour le mélange initial :
xA = 0,36 (Point L) ou xA=0,48 (Point N)
Il suffit d'analyser le solide formé :
si c'est du A pur alors le mélange initial était à xA= 0,48 et si au contraire il s'agit de B pur alors le mélange initial était à xA= 0,36.
Exercice 2 : (R = 8,314 J mol-1 K-1 = 0,082 l atm mol-1 K-1)
Dans un réacteur de 10 litres on introduit une certaine quantité d'oxyde de fer Fe3O4 et 1 mole de monoxyde de carbone CO. On porte ensuite à la température de 1000 K. Il se produit la réaction équilibrée : Fe3O4 (s) + CO (g) = 3 FeO (s) + CO2 (g)
La constante de cet équilibre est K = 1,1 à cette température.
Calculer les pressions partielles de chaque gaz à l'équilibre.
K =( aFeO3 aCO2 ) / ( aFe3O4 aCO ) = PCO2 / PCO
Fe3O4 (s) + CO (g) = 3 FeO (s) + CO2 (g)
E.I : Exces 1 0 0
E.F : Exces 1 - x x x
Nombre de mole gazeuses : ngt = 1 (Pression sans influence)
PCO = (1-x) P
PCO2 = x P
K = 1,1 = x/(1-x)
1,1 (1-x) = x
1,1 - 1,1 x = x
1,1 = 2,1 x
x = 1,1 / 2,1 = 0,524 mole
Calcul de P :
P V = n RT è P = n R T / V = 1 * 0,082 * 1000 / 10 = 8,2 atm = 8,2 bars
Calcul des pressions partielles :
PCO = ( 1 - 0,524) * 8,2 = 3,9 bars
PCO2 = 0,524 * 8,2 = 4,3 bars
Vérifications :
PCO + PCO2 = 3,9 + 4,3 = 8,2 = P
PCO2 / PCO = 4,3 / 3,9 = 1,1 = K
b) Si la quantité de Fe3O4 introduite est de 100g (soit 0,43 mole).
Comme Fe3O4 est solide et n'apparaît donc pas dans la constante d'équilibre rien n'est apparemment modifié par rapport a la question précédante.
On retrouve donc x = 0,524 mole.
Mais a partir de 0,43 mole de Fe3O4 il est impossible d'obtenir 0,524 mole de CO2, on n'atteindra donc pas l'état d'équilibre et la réaction sera totale dans ces conditions.
On obtiendra donc 0,43 mole de CO2 et il restera 1 - 0,43 = 0,57 mole de CO qui n'auront pas réagit.
Soit pour les pressions partielles :
PCO = 0,57 * 8,2 = 4,7 bars
PCO2 = 3,5 bars
Exercice 3 :
Le point de fusion du peroxyde d'hydrogène H2O2 est de -1,7 °C.
Sa chaleur latente de fusion DfusH0 est de 10 Kj mol-1.
Calculer son entropie standard de fusion DfusS0.
DfusS0 = DfusH0 / Tfus
DfusS0 = 10000 / (273 - 1,7) = 36,9 J mol-1 K-1