UNIVERSITE DE LA REUNION

ANNEE UNIVERSITAIRE 2001-2002

Initiation à la CHIMIE THEORIQUE-ATOMISTIQUE

TRAVAUX DIRIGES - Première Période : LES ATOMES

Thierry Briere

PROGRAMME ET RESUME DU COURS

PREMIERE PERIODE : Trois cours (6 h) - Trois séances de Travaux Dirigés ( 6 h)

1) Structure de l’atome

Particules élémentaires (proton-neutron-électron)

Le noyau atomique (Numéro atomique-Nombre de Masse-Isotopie-Energie nucléaire)

Notion de mole et de masse molaire atomique

2) Le cortège électronique (Modèle simple "semi quantique")

a) L’atome d’Hydrogène

Quantification de l’énergie : Spectre de l’Hydrogène

Les 4 nombres quantiques n,l,m,et s

Notion de couche et de sous-couche

b) L’atome polyélectronique

Configuration électronique

Règles de Klechkofsky et de Hund - Principe de Pauli

Modèle simple en couches concentriques

Règles de Slater

Notion de couche de valence

Modèle de Lewis de l’atome

3) La classification périodique des éléments

Présentation - Notion de famille - Prévision des propriétés chimiques

Quelques propriétés atomiques et leur évolution (rayon atomique-Energie d’ionisation-Affinité électronique- Electronégativité-)

EXERCICES

Série 1 : Atomistique

Série 2 : Spectre de l'Hydrogène

Série 3 : Configurations électroniques - Classification périodique

Série 4 : Approximations de Slater - Propriétés atomiques

SERIE 1 : Atomistique

mp = 1,00727 u.m.a mn = 1,00866 u.m.a me = 9,1095 10^-31 kg

N = 6,022 10²³ R_H = 1.097 10⁷ m^-1 h= 6.62 10^-34 Js C = 3 10⁸ ms^-1

Exercice 1 :

Le noyau de l'atome de Lithium est formé de 4 neutrons et trois protons. Calculer en u.m.a la masse théorique de ce noyau. La comparer à sa valeur réelle de 7,01601 u.m.a. Calculer l'énergie de cohésion de ce noyau en J et en MeV.

CORRIGE

Exercice 2 :

Soit la réaction suivante :

2 ²H (deutérium) -----> ³H (tritium) + ¹H

On donne les masses atomiques suivantes en u.m.a :

Hydrogène M=1,.00783 Deutérium M=2,01410 Tritium M=3,01605

a) Quelle quantité d'énergie est libérée par la fusion de 1 kg de deutérium ?

b) Le pouvoir calorifique du charbon est de 33400 KJ Kg^-1, quelle masse de charbon doit-on brûler pour produire l'énergie équivalente à celle produite par la fusion d'un Kg de deutérium ?

CORRIGE

Exercice 3 :

Le Béryllium Be ne possède qu’un seul isotope stable. Sa masse molaire atomique est 9,012 g mol^-1.

a) Calculez l’énergie de cohésion de cet isotope stable, en J mol^-1 puis en MeV par noyau puis en MeV par nucléon.

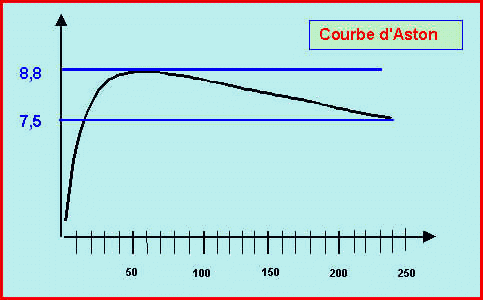
b) On a sommairement représenté la courbe d’Aston. Complétez ce schéma en indiquant les grandeurs représentées (et leurs unités !) en abscisses et en ordonnée. Que représentent les deux traits horizontaux ? Placer approximativement cet isotope sur la courbe. Fait-il parti des isotopes les plus stables ? Si non, par quel type de processus peut-il se stabiliser ?

c) Cet isotope est utilisé comme " générateur de neutrons " dans l’industrie nucléaire. Un atome de cet isotope fixe en effet une particule a , un neutron est libéré et il se forme un autre noyau dont on précisera la nature exacte. Ecrire la transformation correspondante. Est-elle en accord avec la réponse à la question précédante?

Il existe également trois isotopes radioactifs du Béryllium ⁷Be , ⁸Be et ¹⁰Be.

d) L'isotope ⁸Be est émetteur de type a ce qui peut paraître surprenant puisque ce type de radioactivité est généralement observé pour les atomes lourds de Z > 84. Qu’a-t-il de particulier qui justifie cette forme de radioactivité ? Ecrire la réaction nucléaire correspondante.

e) Les deux autres isotopes sont des émetteurs de type b. Attribuez à chacun son type de radioactivité b⁺ ou b^- en justifiant simplement la réponse. Ecrire les réactions nucléaires correspondantes.

Le Magnésium (Z=12) possède trois isotopes stables ²⁴Mg, ²⁵Mg et ²⁶Mg leurs abondances naturelles sont respectivement : 78,6% - 10,1 % et 11,3% . Calculer la masse molaire atomique approchée du Magnésium et expliquer pourquoi le résultat obtenu n’est qu’approximatif.

CORRIGE

Spectre de l’Hydrogène et des Hydrogénoïdes

Exercice 1 :

Si l’électron de l’Hydrogène est excité au niveau n=4, combien de raies différentes peuvent-elles être émises lors du retour à l’état fondamental. Calculer dans chaque cas la fréquence et la longueur d’onde du photon émis.

CORRIGE

Exercice 2:

Si un atome d’Hydrogène dans son état fondamental absorbe un photon de longueur d’onde l₁ puis émet un photon de longueur d’onde l₂, sur quel niveau l’électron se trouve t-il après cette émission ?

a) l₁ = 97,28 nm et l₂ = 1879 nm

b) l₁ = 97,28 nm et l₂ = 78,15 nm

 CORRIGE

Exercice 3 :

Le Lithium présente dans son spectre d’émission une raie rouge intense de longueur d’onde 671 nm.

Calculer l’énergie associée à cette longueur d’onde.

La figure suivante donne les niveaux d’énergies de l’atome de Lithium déterminés à partir de son spectre d’émission.

• Pourquoi le niveau 2s est-il pris comme niveau zéro pour l’énergie ?
• Que représente la valeur 5,37 eV ?
• A quelle transition électronique peut être attribuée la raie d'émission rouge ( l = 671 nm) du spectre du Lithium ?

CORRIGE

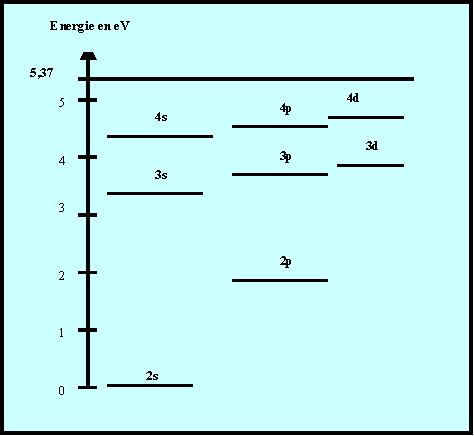
Configurations électroniques - Nombres Quantiques -

Notion de Couche et de sous-couche - Classification périodique

Exercice 1 :

Etablir les configurations électroniques des atomes suivants.Vérifier le résultat obtenus sur une classification périodique. Justifier les éventuelles anomalies.

Ca (Z=20) - Fe(Z=26) - Br(Z=35) - Cs(Z=55) - Cr (Z=24) - Mo (Z=42) - Au (Z=79) -

CORRIGE

Exercice 2 :

Les affirmations suivantes sont-elles exactes ou inexactes? Pourquoi ?

a) Si l=1, l’électron est dans une sous couche d.

b) Si n=4 l’électron est dans la couche O.

c) Pour un électron d, m peut être égal à 3.

d) Si l=2, la sous-couche correspondante peut recevoir au plus 6 électrons

e) Le nombre n d’un électron d’une sous-couche f peut être égal à 3.

f) Si deux " édifices atomiques " ont la même configuration électronique, il s’agit forcément du même élément.

g) Si deux " édifices atomiques " ont des configurations électroniques différentes il s’agit forcément de deux éléments différents.

CORRIGE

Exercice 3:

Un élément a moins de 18 électrons et possède 2 électrons célibataires. Quelles sont les configurations électroniques possibles pour cet élément ? Quel est cet élément sachant qu'il appartient à la période du lithium(3) et au groupe de l'étain(50).

CORRIGE

Exercice 4 :

Les alcalino-terreux

On connaît actuellement 6 éléments appartenant à cette famille qui sont (classés par ordre croissant de leur numéro atomique) : Béryllium – Magnésium - Calcium – Strontium – Baryum et Radium.

1) Quelle colonne de la classification périodique occupe la famille des alcalino-terreux ?

2) Donnez à chacun son numéro atomique et sa configuration électronique.

3) Un autre élément devrait normalement appartenir à cette famille mais en a été exclu. Lequel et pour quelle raison ?

4) Si l’on réussit un jour à obtenir un septième alcalino-terreux quels seront son numéro atomique et sa configuration électronique ?

5) Quel type d’ion donnent les alcalino-terreux ?

6) Quelles sont les formules des oxydes des alcalino-terreux sachant qu’il s’agit de composés ioniques ?

7) Ces oxydes sont-ils acides ou basiques ?

CORRIGE

Approximations hydrogénoïdes de Slater - Propriétés atomiques

Exercice 1 :

On donne les valeurs expérimentales des énergies de première ionisation des éléments de la 2° période EI1 exprimées en Kjmol-1

Li(3) 520 - Be(4) 899 - B(5) 800 - C(6) 1086 - N(7) 1402 - O(8) 1314 - F(9) 1678 - Ne(10) 2084 -

a)Comment passe-t-on des kJmol-1 aux eV ?

b) Convertir ces energies en eV.

c) Par utilisation de l’approximation hydrogénoïde de Slater calculer ces énergies de première ionisation.

d) Comparer les valeurs expérimentales aux valeurs obtenues par le calcul.

e) Justifier les écarts observés par comparaison des schémas de Lewis (sous forme de cases quantiques) des " atomes neutres " et des ions correspondants.

CORRIGE

Exercice 2:

Classer les atomes suivante par rayon atomique croissant :

S(16) ; Mg(12) ; F(9) ; Be(4) ; O(8) ; Si(14)

a) Par simple comparaison des n²/Z*

b) En utilisant la formule R (A°) = 0,215 (n²/Z*) + 0,148 n + 0,225

c) Comparer aux valeurs données par les tables. Conclusion ?

 CORRIGE

Exercice 3:

Classer les éléments suivants par électronégativité croissante :

a) O ; Li et N b) Si ; P ; Cl ; Na et S c) I ; Cl ; F et Br

CORRIGE

Exercice 4 :

Pour évaluer les rayons ioniques Pauling a supposé que ceux-ci étaient proportionnels à n²/Z* comme les atomes neutres. D’autre part il a supposé que dans les cristaux ioniques les anionset les cations étaient au contact et que la distance internucléaire d accessible par diffraction des rayons X etait égale à la somme des rayons ioniques de l’anion et du cation.

Dans NaF d = 2.31 A° : Evaluer les rayons ioniques de Na et F

Dans LiF d = 2.01 A° : Evaluer les rayons ioniques de Li et F

Comparer les valeurs obtenues pour F. Conclusion.

CORRIGE

Exercice 5 :

Soit 4 éléments X, Y, Z et W.

On sait que ces 4 éléments sont situés dans les 3 premières lignes de la classification périodique.

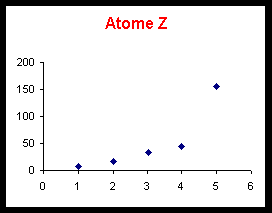
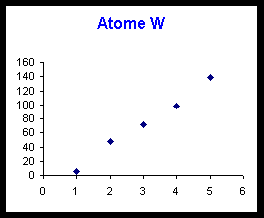
On donne les 5 premières énergies d’ionisation (en eV) de ces quatres éléments.

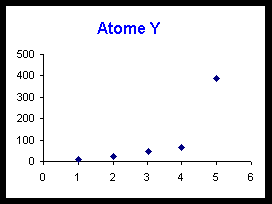
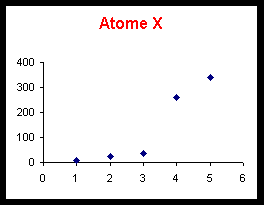
On donne d’autre part une représentation graphique de la variation de ces énergies d’ionisation.

Voir tableau et courbes pages suivantes.

1) Identifiez pour chacun de ces éléments sa colonne dans la classification.

2) Pour un de ces 4 éléments on peut sans hésitation attribuer aussi sa ligne dans la classification. De quel élément s’agit-il ? Donner son symbole chimique et son nom.

3) Deux de ces éléments appartiennent à un même groupe de la classification, comment cela se traduit-il sur la représentation graphique ?

Attribuer à ces deux atomes leur symbole et leur nom.

4) Enfin l’attribution certaine d’une ligne est difficile pour un de ces éléments.

Lequel ? Proposer pour cet élément les deux possibilités pour son symbole et son nom.Pour lever l’indétermination sur la nature de cet élément calculer ses trois premières énergies d’ionisation par les approximations hydrogénoïdes de Slater. Identifier cet élément par comparaison avec les valeurs expérimentales.

5) Pour l’atome Y sur le graphique on constate que les énergies d’ionisation successives se répartissent en deux groupes de deux (EI₁ et EI₂) (EI₃ et EI₄) ; EI₅ étant très différente. Justifiez cette répartition.

CORRIGE

Exercice 6 : Les éléments de la colonne 14

Les éléments de la colonne 14 de la classification périodique sont dans l'ordre de leur numéro atomique croissant : Carbone - Silicium - Germanium - Etain - Plomb

Le tableau suivant résume quelques données sur ces éléments :

1. Complétez le tableau suivant :

1. Nom	Symbole	Z	Configuration électronique simplifiée [gaz rare] (couches externes)	Z*
   Carbone
   Silicium
   Germanium
   Etain
   Plomb

Modèle de Bohr des atomes hydrogénoïdes : (Aucune démonstration n'est demandée)

Enoncer le postulat de Bohr

Donner l'expression obtenue pour le rayon d'une orbite de Bohr.

Donner l'expression obtenue pour l'énergie de l'électron sur une orbite de Bohr.

Que deviennent les deux expressions précédantes dans le cadre du modèle des approximations hydrogénoïdes de Slater.

Rayons de covalence et rayons atomiques

On évalue parfois le rayon atomique par l'expression R_a = a₀ * n² / Z*

Calculer en utilisant cette expression les rayons atomiques des éléments de la colonne 14.

Donner la définition du rayon de covalence d'un atome.

Représenter graphiquement l'évolution du Rayon de covalence en fonction du rayon atomique (définit comme précédemment) pour les éléments de la colonne 14.

Existe-t-il une relation de proportionnalité entre rayon de covalence et rayon atomique pour les éléments de la colonne 14 ?

En fait, pour "améliorer "le modèle de Slater on utilise des valeurs "corrigées" de n notées n*. Pour n = 1, 2 ou 3 on a simplement n* = n, pour n = 4 on prend n* = 3,7 et pour n = 5 on prend n* = 4. Sur le graphique précédant faire figurer les points obtenus en utilisant ces valeurs corrigées de n.

Le résultat obtenu est-il plus satisfaisant ?

Quelle valeur faut-il donner à n* quand n = 6 ?

3) Rayons ioniques :

3-1: Pour chaque rayon ionique de la table fournie donner la nature de l'ion correspondant. Justifier vos réponses.

 CORRIGE