CINETIQUE CHIMIQUE
Exercice 1 :
On étudie la réaction d'hydrolyse d'un composé organochloré :
RCl + H2O = ROH + Cl- + H3O+
Dans une première expérience, on met RCl en solution dans de l'eau pure et on suit l'évolution de la concentration de RCl en fonction du temps. La température est maintenue constante et égale à 35°C. On obtient les résultats suivants :
|
t(min) |
C(mol.L-1) |
t(min) |
C(mol.L-1) |
|
0 |
0,100 |
14 |
0,038 |
|
2 |
0,087 |
15 |
0,036 |
|
4 |
0,076 |
20 |
0,025 |
|
6 |
0,066 |
30 |
0,013 |
|
8 |
0,058 |
45 |
0,004 |
|
10 |
0,050 |
60 |
0,002 |
|
12 |
0,044 |
|
|
- Déterminer l'ordre de cette réaction par rapport à RCl et la valeur de la constante apparente de vitesse.
Cette constante est-elle la valeur réelle de la constante de vitesse de la réaction ? Pourquoi ?
Méthode graphique :
|
t(min) |
C(mol.L-1) |
1/C (L.mol-1) |
ln C |
|
0 |
0,1 |
10,00 |
2,30 |
|
2 |
0,087 |
11,49 |
2,44 |
|
4 |
0,076 |
13,16 |
2,58 |
|
6 |
0,066 |
15,15 |
2,72 |
|
8 |
0,058 |
17,24 |
2,85 |
|
10 |
0,05 |
20,00 |
3,00 |
|
12 |
0,044 |
22,73 |
3,12 |
|
14 |
0,038 |
26,32 |
3,27 |
|
15 |
0,036 |
27,78 |
3,32 |
|
20 |
0,025 |
40,00 |
3,69 |
|
30 |
0,013 |
76,92 |
4,34 |
|
45 |
0,004 |
250,00 |
5,52 |
|
60 |
0,002 |
500,00 |
6,21 |
RCl + H2O = ROH + Cl- + H3O+
v = - d [RCl] / dt = k [RCl]
a [H2O]b
Dans cette expérience l'eau est le sovant en très grand excés, sa concentration est donc constante.
v = - d [RCl] / dt = k [H2O]
b [RCl]a = kap [RCl]a
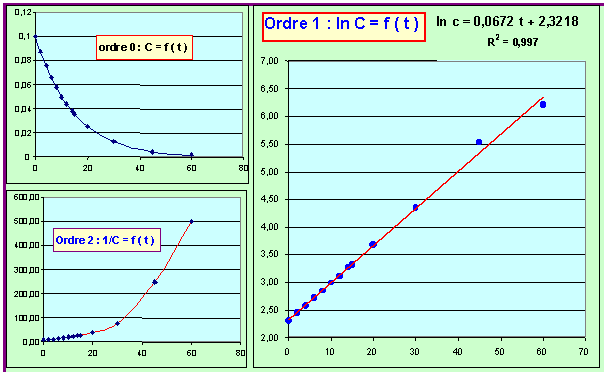
Si on trace ln C = f (t) on obtient une droite, la réaction est donc du premier ordre par rapport à RCl.
La pente de le droite correspond a la constante apparente de la réaction dans les conditions utilisées.
kap = k [H2O]
b = 0,0672 min-1
Méthode calculatoire :
|
t(min) |
C(mol.L-1) |
Ordre 1 |
Ordre 2 |
Ordre 0 |
|
0 |
0,1 |
ln(C/C0)/t |
(1/C-1/C0)/t |
(C-C0)/t |
|
2 |
0,087 |
-0,070 |
0,747 |
-6,500E-03 |
|
4 |
0,076 |
-0,069 |
0,789 |
-6,000E-03 |
|
6 |
0,066 |
-0,069 |
0,859 |
-5,667E-03 |
|
8 |
0,058 |
-0,068 |
0,905 |
-5,250E-03 |
|
10 |
0,05 |
-0,069 |
1,000 |
-5,000E-03 |
|
12 |
0,044 |
-0,068 |
1,061 |
-4,667E-03 |
|
14 |
0,038 |
-0,069 |
1,165 |
-4,429E-03 |
|
15 |
0,036 |
-0,068 |
1,185 |
-4,267E-03 |
|
20 |
0,025 |
-0,069 |
1,500 |
-3,750E-03 |
|
30 |
0,013 |
-0,068 |
2,231 |
-2,900E-03 |
|
45 |
0,004 |
-0,072 |
5,333 |
-2,133E-03 |
|
60 |
0,002 |
-0,065 |
8,167 |
-1,633E-03 |
On voit que l'ordre est bien de 1 et k moyen = 0,069 min-1, résultats proches de la méthode graphique.
- Au bout de combien de temps la concentration de RCl sera-t-elle de 0,01 mol.L-1 ?
Ln (C / C0) = - k t
C = 0,01 C0 = 0,1 C/C0 = 0,01/0.1 = 0,1 t = -ln 0,1 / 0,0672 = 34 minutes
3) Au cours d'une autre expérience la température est maintenue constante et égale à 25°C. On constate que la concentration de RCl est divisée par deux au bout de 22 minutes. Déterminer la constante de vitesse apparente a cette température et l'énergie d'activation de cette réaction.
Ln (C / C0) = - k t
C = 0,01 C0 = 0,1 C/C0 = 0,01/0.1 = 0,1 t = -ln 0,1 / 0,0672 = 34 minutes
C/C0 = 0,5
Ln (C / C0) = -0,693
k = -Ln (C / C0) / t = 0,0315 min-1
Loi d'Arhénius :
k = A exp (-Ea / RT)
ou ln k = ln A – (Ea/RT)
ln k 1= ln A – (Ea/RT1)
ln k2= ln A – (Ea/RT2)
ln k 1 - ln k2 = -(Ea/RT1) + (Ea/RT2) = Ea/R (1/T2 -1/T1)
ln (k1/k2) = (Ea/R) (1/T2 -1/T1)
(Ea /R ) = ln (k1/k2) / (1/T2 -1/T1)
Ea = R ln (k1/k2) / (1/T2 -1/T1)
Ea = 8,31 ln (0,0672/0,0315) / (1/298 -1/308) = 57791 J.mol-1
Exercice 2 :
Etude cinétique de la décomposition de l'eau oxygénée (H2O2)
On donne les potentiels de référence des couples d'oxydoréduction suivants :
Couple H2O2 / H2O E0 = 1,8 V - Couple O2 / H2O2 E0 = 0,7 V - Couple MnO4- / Mn2+ E0=1,5 V
1) Pour la molécule d'eau oxygénée (H2O2), les nombres d'oxydation des atomes d'oxygène sont :
O(-I)
2) On étudie, à T = 300 K, la cinétique de la réaction de décomposition de l'eau oxygénée (H2O2) :
H2O2 = H2O + 1/2 O2
L'évolution de la concentration de l'eau oxygénée (H2O2) au cours du temps est suivie par manganimétrie en milieu acide (pH=0), en titrant 10 mL de solution d'eau oxygénée par une solution 0,02 mol.L-1 de permanganate de potassium ( K+-MnO4- ).
On obtient les résultats :
|
t (min) |
CH2O2 (mol.L-1) |
t (min) |
CH2O2 (mol.L-1) |
|
0 |
0,060 |
20 |
0,024 |
|
5 |
0,048 |
25 |
0,020 |
|
10 |
0,038 |
30 |
0,015 |
|
15 |
0,030 |
35 |
0,013 |
2
-1) Pour le titrage des 10 mL de la solution initiale d'eau oxygénée ( t = 0 - C0 = 0,060 mol.L-1 ) par la solution de KMnO4 0,02 mol.L-1, quel volume a-t-il fallu verser pour atteindre le point équivalent ?
(1) MnO4- + 8 H+ + 5 e- = Mn2+ + 4 H2O
(2) H2O2 = O2 + 2 H+ + 2 e-
Nombre d'e- libéré par H2O2 = Nombre d'e- captés par MnO4-
5 C1 V1 = 2 C2 V2
V1 = 2*0,06*10/5/0,02 = 12 mL
2-2) Quel est L'ordre de la réaction par rapport à H2O2 ?
Méthode graphique
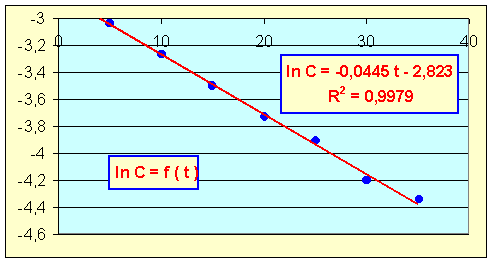
On obtient une droite en portant ln C en fonction du temps, l'ordre est donc de 1 par rapport à H2O2.
2-3) Quelle est La constante de vitesse de la réaction ?
v =- d[H2O2]/dt = k [H2O2]
d[H2O2]/ [H2O2] = - k dt
Ln [H2O2] = - kt + cte
t=0 C=C0
è Cte = ln C0
Ln [H2O2] = - kt + ln C0
k = pente de la droite = 0,0445 min-1
Méthode calculatoire :
|
t (min) |
CH2O2 (mol.L-1) |
Ordre 0 |
Ordre 1 |
Ordre 2 |
|
0 |
0,06 |
(C-C0)/t |
ln(C/C0)/t |
(1/C-1/C0)/t |
|
5 |
0,048 |
-0,0024 |
-0,0446 |
0,8333 |
|
10 |
0,038 |
-0,0022 |
-0,0457 |
0,9649 |
|
15 |
0,03 |
-0,0020 |
-0,0462 |
1,1111 |
|
20 |
0,024 |
-0,0018 |
-0,0458 |
1,2500 |
|
25 |
0,02 |
-0,0016 |
-0,0439 |
1,3333 |
|
30 |
0,015 |
-0,0015 |
-0,0462 |
1,6667 |
|
35 |
0,013 |
-0,0013 |
-0,0437 |
1,7216 |
On retrouve bien l'ordre 1 avec une valeur moyenne k = 0,0452, résultat sensiblement identique à la méthode graphique.
2- 4) Quel temps faut-il pour que 60 % de l'eau oxygénée initiale ait disparu ?
Ln [H2O2] = - kt + ln C0
Ln C = - kt + ln C0
Ln C/C0 = - kt
t = -1/k Ln (C/C0)
C = 0,4 C0
C /C0= 0,4
t = -1/0,0445 Ln (0,4) = 20,6 min = 20 min 35 s
2- 5) Si la solution d'eau oxygénée de départ avait été 2 fois moins concentrée, comment aurait varié la constante de vitesse ?
La constante de vitesse ne dépend pas de la concentration initiale.
Exercice 3 :
On suit la réaction 2 A = B + D à T=cte = 35°C, on détermine par dosage la concentration d'une des espèces (A, B ou D) en fonction du temps. On obtient les résultats suivants :
|
T (min) |
C (mol.L-1) |
T (min) |
C (mol.L-1) |
|
5 |
0,00321027 |
40 |
0,00091575 |
|
10 |
0,00236407 |
45 |
0,00083091 |
|
15 |
0,00187091 |
50 |
0,00076046 |
|
20 |
0,00154799 |
55 |
0,00070102 |
|
25 |
0,00132013 |
60 |
0,0006502 |
|
30 |
0,00115075 |
65 |
0,00060624 |
|
35 |
0,00101989 |
|
|
- Quelle est l'espèce titrée ?
La concentration diminuant au cours du temps, l'espèce titrée est un réactif, donc A.
- Quel est l'ordre de la réaction par rapport à l'espèce A ?
On obtient une droite en portant 1/C en fonction du temps, l'ordre est donc de 2 par rapport à A.
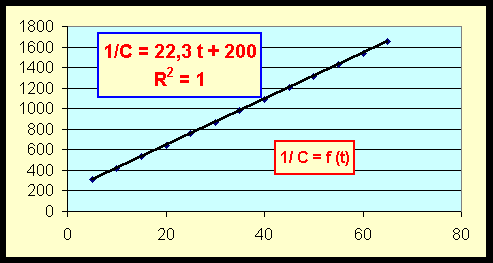
- Quelle est la concentration initiale ?
V = -dA / dt = k [A]2
-dA / dt = k C2
-dA / C2 = k dt
1 / C = k t + Cte
à t = 0, C = C0
è Cte = 1/C0
1/C = k t + 1/C0
On a 1/ C0 = 200 soit C0 = 1/200 = 5 10-3 mol.L-1
- Quelle est la constante de vitesse ?
k = pente de la droite = 22,3 L.mol-1.min-1
- En supposant que l'énergie d'activation de cette réaction soit de 150 KJ.mol-1 que vaudrait cette constante de vitesse à T=70°C ?
Loi d'Arhénius :
k = A exp (-Ea / RT)
ou ln k = ln A – (Ea/RT)
ln k 1= ln A – (Ea/RT1)
ln k2= ln A – (Ea/RT2)
ln k 1 - ln k2 = -(Ea/RT1) + (Ea/RT2) = Ea/R (1/T2 -1/T1)
ln (k1/k2) = (Ea/R) (1/T2 -1/T1)
ln (k1/k2) = (150000/8,31) (1/343 -1/308) = -5,98
k1/k2 = exp(-5,98) = 0,00253
k2 = 22,3/0,00253 = 8819 L.mol-1.min-1
- Au bout de combien de temps 95% de A auront-ils disparus à T = 25°C ?
ln (k1/k2) = (150000/8,31) (1/298 -1/308) = 1,97
k1/k2 = exp(1,97) = 7,15
k2 = 22,3/7,15 = 3,12 L.mol-1.min-1
1/C = k t + 1/C0
k t = 1/ C - 1/ C0
On prend C0 = 5 10-3 mol.L-1
C = 0,05 C0 = 2,5 10-4 mol.L-1
k t = 1/ C - 1/ C0 = 3800
t = 3800/3,12 = 1218 min
- Quel serait le temps de demi-vie si on procédait à la même cinétique à T=35 °C mais en modifiant la concentration initiale en prenant C0 = 0,015 mol.L-1 ?
k t = 1/ C - 1/ C0
On prend C0 = 0,015 mol.L-1
C = 0,5 C0 = 0,0075 mol.L-1
k t = 1/ C - 1/ C0 = 66,67
t = 66,67/22,3 = 3 min


