ENONCES DES EXERCICES DE CHIMIE THEORIQUE
PREMIERE PERIODE - ATOMES
Atomistique
Exercice 1 :
Le noyau de l'atome de Lithium est forme de 4 neutrons et trois protons. Calculer en u.m.a la masse theorique de ce noyau. La comparer a sa valeur reelle de 7,01601 u.m.a. Calculer l'energie de cohesion de ce noyau en J et en MeV.
(mp = 1,00727 u.m.a mn = 1,00866 u.m.a C = 3 108 ms-1 N = 6,022 1023)
Exercice 2 :
Soit la reaction suivante :
2 2H (deuterium) -----> 3H (tritium) + 1H
On donne les masses atomiques suivantes en u.m.a :
Hydrogene M = 1.00783 Deuterium M = 2.01410 Tritium M = 3.01605
a) Quelle quantite d'energie est liberee par la fusion de 1 kg de deuterium ?
b) Le pouvoir calorifique du charbon est de 33400 KJ Kg-1, quelle masse de charbon doit-on brûler pour produire l'energie equivalente a celle produite par la fusion d'un Kg de deuterium ?
Exercice 3 :
Le Magnesium (Z = 12 ) existe sous forme de trois isotopes de nombre de masse 24, 25 et 26. Les fractions molaires dans le magnesium naturel sont respectivement : 0,101 pour 25Mg et 0,113 pour 26Mg.
a) Determiner une valeur approchee de la masse molaire atomique du Magnesium naturel.
b) Pourquoi la valeur obtenue n’est-elle qu’approchee ?
Exercice 4 :
Le chlore naturel est un melange de deux isotopes 35Cl et 37Cl dont les proportions relatives sont respectivement en nombre d’atomes 75% et 25%.
a) Calculer la masse molaire atomique du Chlore naturel.
b) Combien de sortes de molecules de dichlore existe-t-il dans le dichlore naturel ?
c) Quelles sont leur masse molaire respectives et leur proportions relatives dans le dichlore naturel ?
Spectre de l’Hydrogene et des Hydrogenoides
Exercice 1 :
Si l’electron de l’Hydrogene est excite au niveau n=4, combien de raies differentes peuvent-elles etre emises lors du retour a l’etat fondamental. Calculer dans chaque cas la frequence et la longueur d’onde du photon emis.
(RH = 1.097 107 m-1 h = 6.62 10-34 Js C = 3 108 ms-1)
Exercice 2:
Si un atome d’Hydrogene dans son etat fondamental absorbe un photon de longueur d’onde ?1 puis emet un photon de longueur d’onde l2, sur quel niveau l’electron se trouve-t-il apres cette emission ?
a) l1 = 97.28 nm et l2 = 1879 nm
b) l1= 97.28 nm et l2 = 78.15 nm
Exercice 3 :
Le spectre de l’atome d’hydrogene peut se decomposer en plusieurs series de raies nommees pour les quatre premieres : series de Lyman ; de Balmer ; de Paschen et de Pfund.
a) Expliquer a quoi correspondent ces diverses series.
b) Les longueurs d’onde des raies de chaque serie sont comprises entre deux valeurs limites. A quoi correspondent ces deux limites ?
c) Donner une formule generale permettant le calcul de ces deux limites.
d) Calculer les longueurs d’ondes limites des series de Lyman, Balmer , de Paschen et de Pfund.
e) Attribuer a chaque serie son domaine spectral (U.V ; Visible ; I.R).
Configurations electroniques
Etablir les configurations electroniques des atomes suivants. Verifier le resultat obtenus sur une classification periodique. Justifier les eventuelles anomalies.
Ca (Z=20) - Fe(Z=26) - Br(Z=35) - Cs(Z=55) - Cr (Z=24) - Mo (Z=42) - Au (Z=79)
Nombres Quantiques
Les affirmations suivantes sont-elles exactes ou inexactes? Pourquoi ?
a) Si l=1, l’electron est dans une sous couche d.
b) Si n=4 l’electron est dans la couche O.
c) Pour un electron d, m peut etre egal a 3.
d) Si l=2, la sous-couche correspondante peut recevoir au plus 6 electrons
e) Le nombre n d’un electron d’une sous-couche f peut etre egal a 3.
f) Si deux " edifices atomiques " ont la meme configuration electronique, il s’agit forcement du meme element.
g) Si deux " edifices atomiques " ont des configurations electroniques differentes il s’agit forcement de deux elements differents.
CLAS
Classification Periodique des Elements
Exercice 1 :
Indiquez en le justifiant le nombre d'elements presents dans les 1ere, 2eme, 3eme , 4eme, 5eme et 6eme periodes de la classification. Indiquez dans chaque cas le nombre d'elements de transition.
Exercice 2:
Un element a moins de 18 electrons et possede 2 electrons celibataires. Quelles sont les configurations electroniques possibles pour cet element ? Quel est cet element sachant qu'il appartient a la periode du lithium(3) et au groupe de l'etain(50).
Exercice 3 :
Un compose ionique a pour formule A2B3
On sait que les elements A et B sont tous deux des elements des deuxieme ou troisieme periodes de la classification. On sait d’autre part que l’element A est un METAL alors que B est un NON-METAL (ou METALLOIDE).
Quelles sont les natures possibles pour ce compose ionique ?
- On rappelle que selon la regle de Sanderson un element est considere comme metallique si le nombre total d’electron de sa couche de valence est inferieur ou egal au numero de la periode auquel il appartient.
- On suppose que la charge d’un ion est toujours entiere.
- On suppose que les ions sont les ions les plus stables de l’element correspondant.
Approximations hydrogenoides de Slater - Proprietes atomiques
Exercice 1 :
On donne les valeurs experimentales des energies de premiere ionisation des elements de la deuxieme periode EI1 exprimees en Kj mol-1
Li |
Be |
B |
C |
N |
O |
F |
Ne |
520 |
899 |
800 |
1086 |
1402 |
1314 |
1678 |
2084 |
a)Comment passe-t-on des kJ mol-1 aux eV ?
b) Convertir ces energies en eV.
c) Par utilisation de l’approximation hydrogenoide de Slater calculer ces energies de premiere ionisation.
d) Comparer les valeurs experimentales aux valeurs obtenues par le calcul.
e) Justifier les ecarts observes par comparaison des schemas de Lewis (sous forme de cases quantiques) des " atomes neutres " et des ions correspondants.
Exercice 2 :
Pour l’atome de Chlore evaluer :
a) l’energie d’ionisation (Cl -->Cl+)
b) l’energie de fixation electronique (Cl --->Cl-)
c) l’electronegativite dans l’echelle de Mulliken : XM = 0.21 (EI + EA)
d) le rayon de covalence : R (A°) = 0,215 (n2/Z*) + 0,148 n + 0,225
e) l’electronegativite dans l’echelle d’Alred et Rochow.
XA-R= 0,34 (Z*/R2 )+ 0.67 (R en A°)
f) Comparer les valeurs calculees aux valeurs donnees dans les tables.
Exercice 3 :
Classer les atomes suivante par rayon atomique croissant :
S(16) ; Mg(12) ; F(9) ; Be(4) ; O(8) ; Si(14)
a) Par simple comparaison des n2/Z*
b) En utilisant la formule R (A°) = 0,215 (n2/Z*) + 0,148 n + 0,225
c) Comparer aux valeurs donnees par les tables. Conclusion ?
Exercice 4:
Classer les elements suivants par electronegativite croissante :
a) O ; Li et N
b) Si ; P ; Cl ; Na et S
c) I ; Cl ; F et Br
Exercice 5 :
Pour evaluer les rayons ioniques Pauling a suppose que ceux-ci etaient proportionnels a n2/Z* comme les atomes neutres. D’autre part, il a suppose que dans les cristaux ioniques les anions et les cations etaient au contact et que la distance internucleaire d accessible par diffraction des rayons X etait egale a la somme des rayons ioniques de l’anion et du cation.
Dans NaF d = 2.31 A° : Evaluer les rayons ioniques de Na et F
Dans LiF d = 2.01 A° : Evaluer les rayons ioniques de Li et F
Comparer les valeurs obtenues pour F. Conclusion.
Exercice 6 :
Soit 4 elements X, Y, Z et W.
On sait que ces 4 elements sont situes dans les 3 premieres lignes de la classification periodique.
On donne les 5 premieres energies d’ionisation (en eV) de ces quatre elements.
On donne d’autre part une representation graphique de la variation de ces energies d’ionisation.
| E.I | Atome X | Atome Y | Atome Z | Atome W |
| 1 | 8,26 | 11,22 | 8,12 | 5,14 |
| 2 | 25 | 24,27 | 16,27 | 47,3 |
| 3 | 37,75 | 47,65 | 33,35 | 71,6 |
| 4 | 258,1 | 64,22 | 44,93 | 98,9 |
| 5 | 338,5 | 390,1 | 156,6 | 138,4 |
1) Identifiez pour chacun de ces elements sa colonne dans la classification.
2) Pour un de ces 4 elements on peut sans hesitation attribuer aussi sa ligne dans la classification. De quel element s’agit-il ? Donner son symbole chimique et son nom.
3) Deux de ces elements appartiennent a un meme groupe de la classification, comment cela se traduit-il sur la representation graphique ?
Attribuer a ces deux atomes leur symbole et leur nom.
4) Enfin l’attribution certaine d’une ligne est difficile pour un de ces elements. Lequel ? Proposer pour cet element les deux possibilites pour son symbole et son nom.Pour lever l’indetermination sur la nature de cet element calculer ses trois premieres energies d’ionisation par les approximations hydrogenoides de Slater. Identifier cet element par comparaison avec les valeurs experimentales.
5) Pour l’atome Y sur le graphique on constate que les energies d’ionisation successives se repartissent en deux groupes de deux (EI1 et EI2) (EI3 et EI4) ; EI5 etant tres differente. Justifiez cette repartition.
CORRIGES DES EXERCICES
ATOMISTIQUE
ATOMISTIQUE Exercice 1 :
Masse theorique : Mtheo = 3 mp + 4 mn = 7,05645 u.m.a
La masse reelle est inferieure a la masse theorique. Le defaut de masse Dm correspond a l’energie de cohesion du noyau.
Dm = 0.04044 u.m .a = 0.044044 / N = 6,715 10-29 Kg.
E = Dm C2 = 6,045 10-12 J = 37,8 MeV
Exercice 2 :
2 2H à 3H + 1H
Dm = 3,01605 + 1.00783 – (2 * 2,0141) = -0,00432 u.m.a
Dm = - 0.00432 u.m.a / 2 atomes ou Dm = -0,00432 g / 2 moles
DE = Dm * C2 = - 3.89 1011 J / 2 moles
Le signe negatif indique que l’energie est degagee par cette reaction "exothermique".
Soit 1,94 1011 J / mole ; soit 1,94 1011 J/ 2.0141 g soit 9,65 1013 J / Kg
Masse de charbon equivalente : MC = 9,65 1013 / 33400 103 = 3000 tonnes environ
L’energie degagee par les processus nucleaires est beaucoup plus importante que celle degagee par les processus chimiques ordinaires (ici 3 106 fois plus). Cela explique l’utilisation de l’energie nucleaire malgre les risques potentiels.
Exercice 3 :
Fraction molaire : Correspond au pourcentage en nombre de mole xi = ni / nt et S xi = 1
25Mg : xi = 0,101 ; 26Mg : xi = 0,113 => 24Mg : xi = 1 – 0,101 – 0,113 = 0,786
MMg = 0,101 * 25 + 0,113 * 26 + 0,786 * 24 = 24,3 g.mol-1
Aproximations : mp = mn = 1 u.m.a ; masse des electrons negligee ; defaut de masse neglige.
La comparaison avec les tables montre que les approximations sont legitimes et que le premier chiffre apres la virgule est encore exact (voir classification).
Exercice 4 :
MCl = 0,75 * 35 + 0.25 * 37 = 35,5 g.mol-1
Molecule |
Masse Molaire (Mi) | Abondance (xi) |
35Cl – 35Cl |
70 |
0,75 * 0,75 = 0,5625 |
37Cl – 37Cl |
74 |
0,25 * 0,25 = 0,0625 |
35Cl – 37Cl ou 37Cl – 35Cl |
72 |
2 * 0.25 * 0,75 = 0,375 |
Verifications possibles : S xi = 1 et MCl2 = 2 * 35,5 = 71 = S ( xi Mi )
Spectres de l’Hydrogene et des Hydrogenoides
Exercice 1 :
6 raies possibles :

Modele de Bohr : En = - E0 / n2
Formule de Rydberg : 1/l = RH (1/n2 – 1/p2)
E n,p = -E0 / n2 + E0 / p2 = E0 (1/p2 - 1/n2)
E = h . n et n = C / l
E0 = h C RH = 6,62 10-34 * 3 108 * 1,097 107
E0 = 2,18 10-18 J ( 13,6 eV )
Raie - Transition |
Energie (J) |
Frequence n ( 1015 Hz ) |
Longueur d’onde (nm) |
4 à 3 |
1,06 10-19 |
0,16 |
1874 |
4 à 2 |
4,09 10-19 |
0,62 |
486 |
4 à 1 |
2,04 10-18 |
3,09 |
97,2 |
3 à 2 |
3,02 10-19 |
0,46 |
656 |
3 à 1 |
1,93 10-18 |
2,93 |
102,5 |
2 à 1 |
1,63 10-18 |
2,5 |
121,5 |
Remarque : Une erreur frequente consiste a penser que les niveaux sont equidistants, ce qui ramenerait le nombre de raies a trois seulement.
Exercice 2 :
DE = Em – E1 = E0 ( 1 - 1/m2 )
DE = h (n1 – n2) = h C ( 1/l1 – 1/l2) = h C A
h C RH ( 1 – 1/m2) = h C A
RH ( 1 – 1/ m2 ) = A
1 - 1/m2 = A / RH
1/m2 = 1 – (A / RH)
m2 = 1 / [ 1 – ( A / RH ) ] avec A = 1/l1 – 1/l2
Application numerique :
l’atome ne peut restituer une energie superieure a celle reçue initialement.
Exercice 3 :
Serie : ensemble des raies qui correspondent au retour sur un meme niveau n
Lyman : n = 1 - Balmer : n =2 - Paschen : n = 3 - Pfund : n = 4
Les deux raies limites de chaque serie correspondent au passage Infini à n et au passage n + 1 à n
Passage de l’infini a n :
1 / l1 = RH (1/n2 –1/p2) = RH / n2 => l1 = n2 / RH
Passage de n + 1 a n :
1 / l2 = RH (1/n2 –1/(n+1)2) = RH [ (n + 1)2 - n2] / [n2 (n+1)2] => l2 = n2 (n + 1)2 / [ ( 2n + 1 ) RH]
Serie |
l1 ( nm) |
l2 (nm) |
| Lyman (n = 1) | 91 |
122 |
| Balmer ( n = 2 ) | 365 |
656 |
| Paschen ( n = 3 ) | 820 |
1875 |
| Pfund ( n = 4 ) | 1458 |
4051 |
Remarque :
Les series sont de plus en plus etalees et on observe un chevauchement des n = 4.
On finit donc pour n eleve par obtenir un spectre quasi continu.
Pour certains atomes emettant dans le visible, on pourra donc obtenir une lumiere pratiquement blanche, d’où l’utilisation pour l’eclairage "au neon ".
Visible de 400 a 750 nm.
Voir la representation graphique.
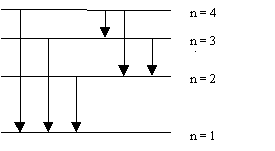
Regle de Klechkowski : A quelques exceptions pres, le remplissage des couches et des sous-couches se fait dans l’ordre des valeurs de ( n + l ) croissant. Si plusieurs combinaisons possibles conduisent a la meme valeur, on choisit celle possedant la plus petite valeur de n .
Soit la representation mnemotechnique suivante :
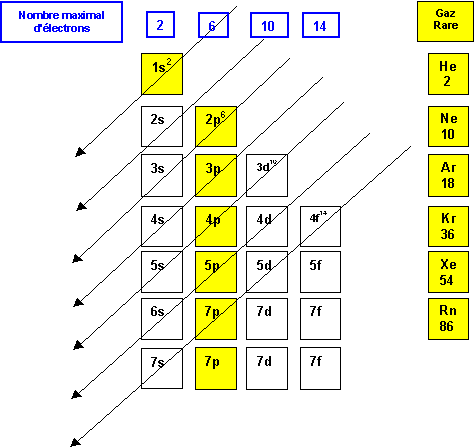
Exercice 1 :
Regle de Klechkowski : A quelques exceptions pres, le remplissage des couches et des sous-couches se fait dans l’ordre des valeurs de ( n + l ) croissant. Si plusieurs combinaisons possibles conduisent a la meme valeur, on choisit celle possedant la plus petite valeur de n .
Soit la representation mnemotechnique suivante :

Calcium (Ca) : Z = 20 = 18 + 2 à ( Ar ) 4s2
Fer (Fe) : Z = 26 = 18 + 8 à ( Ar ) 4s2 3d6 ( Ar ) 3d6 4s2
Brome (Br) : Z = 35 = 18 + 17 à ( Ar ) 4s2 3d10 4p5 ( Ar ) 3d10 4s2 4p5
Cesium (Cs) : Z = 55 = 36 + 19 à ( Ar ) 4s2 3d10 4p6 5s1 ( Ar ) 3d10 4s2 4p6 5s1
Chrome (Cr) : Z = 24 = 18 + 6 à ( Ar ) 4s2 3d4 ( Ar ) 3d4 4s2
Molybdene (Mo) : Z = 42 = 36 + 6 à ( Kr ) 5s2 4d4 ( Kr ) 4d4 5s2
Or (Au) : Z = 79 = 54 + 25 à ( Xe ) 6s2 4f14 5d9 ( Xe ) 4f14 5d9 6s2
Comparaison avec les configurations electroniques reelles :
La regle de Klechkowski ne permet pas d’obtenir a coup sur la configuration electronique reelle des atomes. A partir de n = 3 de nombreuses exceptions a cette regle apparaissent. Nous ne chercherons pas a justifier toutes ces exceptions mais on peut expliquer certaines d’entre elles en admettant qu’une sous-couche totalement remplie ou a demi remplie apporte une stabilite supplementaire.
Ainsi la configuration d5 s1 est-elle plus stable que la configuration d6 s2 ( Cr et Mo)

De meme la configuration d10 s1 est plus stable que la configuration d9 s2 ( Au )
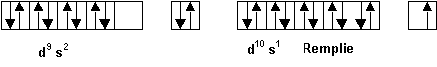
Les configurations reelles de ces trois elements sont donc :
Cr : ( Ar ) 3d5 4s1 Mo : ( Kr ) 4d5 5s1 Au : ( Xe ) 4f14 5d10 6s1
Nous admettrons cette regle et l’appliquerons quand ces cas semblables se presenteront.
Nous rencontrerons des situations analogues lors de l’etude des energies de premiere ionisation et pour expliquer la formation de certains ions.
Remarque : Si la configuration est modifiee la position dans la classification periodique ne l’est pas.
Rappel des regles concernant les 4 nombres quantiques :
n : nombre quantique principal avec n entier non nul n = 1, 2, 3 ….
l : nombre quantique secondaire (ou azimutal) avec l compris entre 0 et n –1
ml (ou m) : nombre quantique magnetique avec m compris entre – l et + l
ms (ou s) : nombre quantique de spin avec ms = 1/2 ou ms = - 1/2
n : couche
l : sous-couche
m : case quantique
Les valeurs de n sont codifiees par des lettres majuscules :
n = 1 à K ; n = 2 à L ; n = 3 à M ; n = 4 à N ; n = 5 à O …
Les valeurs de l sont codifiees par des lettres minuscules :
l = 0 à s ; l = 1 à p ; l = 2 à d ; l = 3 à f ; l = 4 à g …
a) l = 1 à p : FAUX
b) n = 4 à N : FAUX
c) d à l = 2 à ml = -2, -1, 0, 1, 2 : FAUX
d) l = 2 à ml = -2, -1, 0, 1, 2 à 5 cases quantiques à 10 electrons maximum : FAUX
e) n = 3 à l = 0, 1, 2 (s,p,d) à pas de f sur couche 3 : FAUX
f) " edifice atomique " = atome " neutre " ou ion
g) Un ion a la meme configuration electronique qu’un atome neutre d’un autre element : FAUX
Exemples : Na+ , Ne et O2- ont la meme configuration electronique.
h) L’ion et l’atome neutre du meme element ont forcement des configurations electroniques differentes : FAUX
La classification periodique reproduit fidelement la regle de Klechkowski.
Ligne 1 : n = 1 à 2 n2 = 2 (1 s2) à 2 elements.
Ligne 2 : n = 2 à 2 n2 = 8 (2s2 2p6) à 8 elements.
Ligne 3 : n = 3 à 2 n2 = 18 ( 3s2 3p6 3d10 ) à 18 elements prevus mais selon Klechkowski le niveau 3d ne se remplit qu’apres le niveau 4s ; ce niveau sera donc place dans la quatrieme ligne et finalement, il n’y aura que 8 elements dans la troisieme ligne. Les elements de transitions correspondent aux blocs d et f. Ici 10 elements de transition (3d10).
Ligne 4 : n = 4 à 2 n2 = 32 (4s2 4p6 4d10 4f14) à 32 elements prevus mais selon Klechkowski le niveau 4d ne se remplit qu’apres le niveau 5s ; ce niveau sera donc place dans la cinquieme ligne, de meme le niveau 4f ne se remplit qu’apres le niveau 6s ; ce niveau sera donc place dans la sixieme ligne. Il devrait donc y avoir 8 elements dans la quatrieme ligne mais n’oublions pas d’ajouter les elements correspondant au niveau 3d. Finalement, il y aura 18 elements dans la quatrieme ligne, dont 10 de transition.
Ligne 5 : n = 5 à 2 n2 = 50 (5s2 5p6 5d10 5f14 5g18) à 50 elements prevus mais selon Klechkowski le niveau 5d ne se remplit qu’apres le niveau 6s ; ce niveau sera donc place dans la sixieme ligne, de meme le niveau 5f ne se remplit qu’apres le niveau 7s ; ce niveau sera donc place dans la septieme ligne. Le niveau 5g n’est pas utilise pour les elements connus il n’apparaîtrait de toute façon qu’a la huitieme ligne. Il devrait donc y avoir 18 elements dans la cinquieme ligne mais n’oublions pas d’ajouter les elements correspondant au niveau 4d. Finalement, il y aura 18 elements dans la quatrieme ligne, dont 10 de transition.
Ligne 6 : n = 6 à 2 n2 = 72 (6s2 6p6 6d10 6f14 6g18 6h22) à 50 elements prevus mais selon Klechkowski le niveau 6d ne se remplit qu’apres le niveau 7s ; ce niveau sera donc place dans la septieme ligne, de meme le niveau 6f ne se remplit qu’apres le niveau 8s ; ce niveau sera donc place dans la huitieme ligne. Les niveaux 6g et 6h ne seront pas utilises. Il devrait donc y avoir 18 elements dans la cinquieme ligne mais n’oublions pas d’ajouter les elements correspondant au niveaux 5d et 4f. Finalement, il y aura 32 elements dans la quatrieme ligne, dont 24 de transition. Pour des raisons pratiques les niveaux correspondant aux sous couches f sont repousses en bas a droite de la classification.
Remarque : On peut retrouver plus simplement ce principe de construction en considerant que dans la representation de la regle de Klechkowski une ligne demarre toujours par ns.
La ligne 6 demarre donc avec 6s et se termine avec 6p. On retrouve donc 6s2, 4f14, 5d10, 6p6
Soit finalement la representation traditionnelle :
| 1s | |||||||||||||||||
| 2s | 2p | ||||||||||||||||
| 3s | 3p | ||||||||||||||||
| 4s | 3d | 4p | |||||||||||||||
| 5s | 4d | 5p | |||||||||||||||
| 6s | 5d | 6p | |||||||||||||||
| 7s | 6d |
| 4f | |||||||||||||
| 5f |
Exercice 4 :
L’element en question appartient a l’une des trois premieres lignes de la classification.
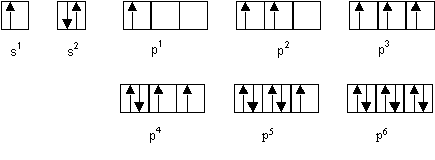
La representation sous forme de cases quantiques montre que seules les configurations p2 et p4 possedent deux electrons celibataires. L’element en question ne peut donc etre que : C, Si, O ou S.
On sait qu’il appartient a la periode du lithium, donc Si et S sont elimines.
Cherchons la configuration de l’etain ( Z = 50)
50 = 36 + 14 à (Kr) 4d10 5s2 5p2
L’element cherche appartenant au meme groupe que l’etain est donc le Carbone C.
s1 |
s2 |
p1 |
p2 |
p3 |
p4 |
p5 |
p6 |
H |
He |
||||||
Li |
Be |
B |
C |
N |
O |
F |
Ne |
Na |
Mg |
Al |
Si |
P |
S |
Cl |
Ar |
Exercice 7 :
Le compose ionique de formule A2B3 contient des ions A et B portant respectivement 3 charges et 2 charges.
Soit les diverses possibilites suivantes :
A3+ et B2- ou A3- et B2+
On sait que les metaux donnent des cations et les non-metaux des anions.
A est donc le cation ( A3+ ) et B l’anion ( B2- ).
A et B appartiennent aux trois premieres periodes.
Les possibilites pour A sont : le Bore ou l’Aluminium.
Les possibilites pour B sont : l’Oxygene ou le Soufre.
La regle de Sanderson permet d’exclure le Bore qui appartient a la periode 2 et possede 3 electrons de valence et n’est donc pas un metal. L’Aluminium possedant 3 electrons de valence et appartenant a la troisieme periode est bien un metal. L’Oxygene et le Soufre sont bien deux metalloides avec leurs 6 electrons de valence.
Il reste donc deux possibilites : Al2O3 et Al2S3.
Approximations hydrogenoides de Slater – Proprietes atomiques
Exercice 1 :
a) KJ / mole * 1000 / N / e à eV / atome
N * e = F = 96500 C
Kj mol-1 / 96,5 à eV/atome
b)
Li |
Be |
B |
C |
N |
O |
F |
Ne |
5,4 |
9,3 |
8,3 |
11,3 |
14,5 |
13,6 |
17,4 |
21,6 |
c) Calcul des energies d’ionisation :
Nous allons montrer sur deux exemples comment on peut calculer la valeur approximative de l’energie d’ionisation grâce aux approximations hydrogenoides de Slater.
Oxygene ( Z = 8 )
| O | 1s2 | 2s2 , 2p4 |
| 2 E1 | 6 E2 | |
| O+ | 1s2 | 2s2 , 2p3 |
| 2 E1 | 5 E'2 |
O à O+ + 1 e-
Energie de premiere ionisation E.I1 = EO+ - EO
E O+ = 2 E1 + 5 E'2
EO = 2 E1 + 6 E2
E.I1 = 5 E'2 - 6 E2
Calcul de Z*E2 et E2 :
Z*E2 = 8 – (5 * 0,35) - (2 * 0,85) = 4,55
E2 = -13.6 * 4,552 / 4 = -70,39 eV
Calcul de Z*E'2 et E'2 :
Z*E'2 = 8 – (4 * 0,35) - (2 * 0,85) = 4,9 (soit plus simplement 4,55 + 0,35 = 4,9)
E'2 = -13.6 * 4,92 / 4 = -81,63 eV
Calcul de E.I1 :
E.I1 = 5 E'2 - 6 E2 = (5 * -81,63) - (6 * -70,39) = 14,2 eV
Carbone ( Z = 6)
| C | 1s2 | 2s2 , 2p2 |
| 2 E1 | 4 E2 | |
| C+ | 1s2 | 2s2 , 2p1 |
| 2 E1 | 3 E'2 |
C à C+ + 1 e-
Energie de premiere ionisation E.I1 = EC+ - EC
E C+ = 2 E1 + 3 E'2
EO = 2 E1 + 4 E2
E.I1 = 3 E'2 - 4 E2
Calcul de Z*E2 et E2 :
Z*E2 = 6 – (3 * 0,35) - (2 * 0,85) = 3,25
E2 = -13.6 * 3,252 / 4 = -35,91 eV
Calcul de Z*E'2 et E'2 :
Z*E'2 = 6 – (2 * 0,35) - (2 * 0,85) = 3,6 (soit plus simplement 3,25 + 0,35 = 3,6)
E'2 = -13.6 * 3,62 / 4 = -44,06 eV
Calcul de E.I1 :
E.I1 = 3 E'2 - 4 E2 = (3 * -44,06) - (4 * -35,91) = 11,5 eV
Le calcul est identique pour les autres elements. On peut meme automatiser le calcul sur calculatrice programmable.
Le principe de calcul est alors le suivant :
| Z | 1s | 2s,2p | Z*1s | Z*2s,2p | E1s | E2s,2p | E totale | E.I | |
| atome | Z | n1 | n2 | Z – 0,3 | Z - (n2-1)*0,35 - 2*0,85 | -13,6 * Z*21s | -13,6 * Z*22s/4 | n1E1s+n2 E2s | |
| ion | Z | n1 | n2 - 1 | Z – 0,3 | Z - (n2-2)*0,35 - 2*0,85 | -13,6 * Z*21s | -13,6 * Z*22s/4 | n1E1s+n2 E2s | Eion-Eatom |
Resultats :
| Valeur experimentaleEcart ( % ) | |||
Li |
5,7 |
5,4 |
6,4 |
Be |
7,9 |
9,3 |
-15,4 |
B |
9,8 |
8,3 |
17,8 |
C |
11,5 |
11,3 |
1,4 |
N |
12,9 |
14,5 |
-10,9 |
O |
14,2 |
13,6 |
4,1 |
F |
15,2 |
17,4 |
-12,8 |
Ne |
16,0 |
21,6 |
-26,0 |
Interpretation :
Cette methode simple de calcul permet d’atteindre l’ordre de grandeur de l’energie de premiere ionisation d’un atome. L’ecart moyen est de 6 %, cette precision est appreciable eu egard a la simplicite du modele utilise. La courbe des valeurs calculees est reguliere alors que la courbe experimentale presente des discontinuites. REPRESENTATION GRAPHIQUE
Cette tendance generale a l’augmentation souffre deux " accidents " correspondant a B et N pour lesquels on observe une diminution de l’energie d’ionisation. On peut comprendre (sinon expliquer) ces accidents en examinant la structure electroniques des atomes et ions correspondants. Rappelons la regle vue a l’exercice 1 : " une couche ou sous-couche a demi remplie ou completement remplie apporte une stabilite supplementaire ".
Si cette regle est respectee, les atomes ayant une couche de ce type seront tres stables et donc difficiles a ioniser puisqu’on perd alors cette stabilite supplementaire ; leur energie d’ionisation sera alors "anormalement elevee ".
Les atomes de ce type sont Be, N et Ne et on trouve effectivement que la valeur experimentale de l’energie d’ionisation est plus elevee que sa valeur calculee.
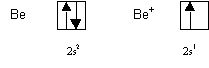

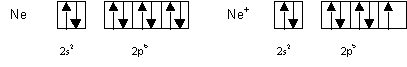
Inversement les ions possedant une couche remplie ou demi remplie seront tres stables et l’atome correspondant aura donc une energie d’ionisation "anormalement faible ".
Les atomes de ce type sont B et O et on trouve effectivement que la valeur experimentale de l’energie d’ionisation est plus faible que sa valeur calculee.
Le carbone n’appartient a aucune de ces categories et son energie d’ionisation calculee est tres proche de la valeur experimentale.
Le Lithium est un cas particulier, sa couche de valence 1s1 le placerait a la limite dans la premiere categorie, mais l’ion forme possede une couche totalement remplie (1s2). C’est cet effet qui l’emporte et on trouve que la valeur experimentale de l’energie d’ionisation est plus faible que sa valeur calculee.
Reste enfin le cas de l’atome de Fluor qui comme le carbone devrait conduire a des valeurs calculee et experimentale proches. Ce n’est pas le cas, et la valeur experimentale est beaucoup plus elevee que la valeur calculee. Le fort ecart observe pour cet atome traduit la difficulte d’arracher des electrons alors qu’il suffirait d’en ajouter un pour atteindre la structure de gaz rare. C’est une manifestation de la regle de l’octet. Enfin, cela traduit aussi la forte electronegativite de l’atome de Fluor qui retient fortement les electrons.
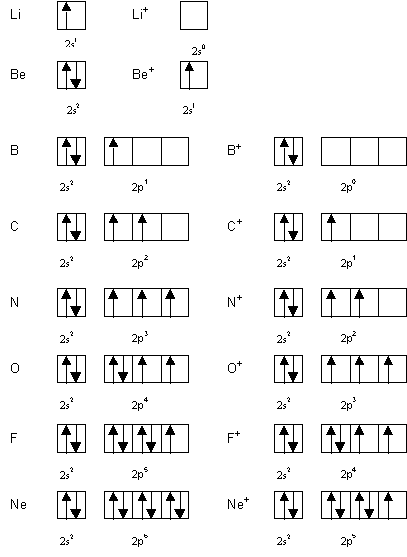
Exercice 2 :
Cl : Z = 17 1s2, 2s2, 2p6, 3s2, 3p5
| Cl | 1s2 | 2s2 2p6 | 3s2 3p5 |
| 2 E1 | 8 E2 | 7 E3 | |
| Cl+ | 1s2 | 2s2 2p6 | 3s2 3p4 |
| 2 E1 | 8 E2 | 6 E'3 | |
| Cl- | 1s2 | 2s2 2p6 | 3s2 3p6 |
| 2 E1 | 8 E2 | 8 E''3 |
ECl = 2 E1 + 8 E2 + 7 E3 ECl+ = 2 E1 + 8 E2 + 6 E’3 ECl- = 2 E1 + 8 E2 + 8 E’3
Cl à Cl+ + e-
E.I = ECl+ - ECl = 6 E’3 – 7 E3 ( E.I = energie d’ionisation )
Cl + e- à Cl-
Efe = ECl- - ECl = 8 E’’3 – 7 E3 ( Efe = energie de fixation electronique)
Z*Cl = 17 – ( 6 * 0,35 ) – ( 8 * 0,85 ) – 2 = 6,1
Z*Cl+ = Z*Cl + 0,35 = 6,45
Z*Cl- = Z*Cl - 0,35 = 5,75
E3 = -13,6 * 6,12 / 9 = -56,22 eV
E’3 = -13,6 * 6,452 / 9 = -62,87 eV
E’’3 = -13,6 * 5,752 / 9 = -49,96 eV
E.I = ( 6 * - 62,87 ) – ( 7 * -56,22 ) = 16,3 eV PROCESSUS ENDOTHERMIQUE - DIFFICILE
Efe = ( 8 * - 49,96 ) – ( 7 * -56,22 ) = -6,1 eV PROCESSUS EXOTHERMIQUE – FACILE
XM = 0,21 * ( 16,3 + 6,1 ) = 4,7
RCl = ( 0,215 * 9 / 6,1) + ( 0,148 * 3 ) + 0,223 = 0,984 A°
XAR = (0,34 * 6,1 / 0,9842) + 0,67 = 2,81
Valeur Calculee |
Valeur Tabulee |
|
E.I |
16,3 |
13 |
E.A |
6,1 |
3,62 |
XM |
4,7 |
3,5 |
R |
0,984 |
0,99 |
XAR |
2,81 |
2,8 |
Conclusions :
L’utilisation des regles de Slater permet d’evaluer simplement l’ordre de grandeur de certaines proprietes atomiques.
L’energie d’ionisation est mieux evaluee que l’affinite electronique. L’ecart entre valeur calculee et valeur experimentale est toutefois assez grand. On n’obtient que l’ordre de grandeur de celles-ci. On peut toutefois tirer des conclusions qualitatives interessantes. Ici on voit bien que l’ionisation "spontanee " de Cl donne Cl- (processus exothermique liberant de l’energie) et non Cl+ (processus endothermique necessitant un apport d’energie) ce qui est tout a fait conforme a l’experience.
L’electronegativite de Mulliken est assez mal evaluee en raison des erreurs sur EI et EA mais on voit tout de meme que Cl est un atome fortement electronegatif. Si on verifie sur une table on trouve effectivement que Cl est l'atome le plus electronegatif (hormis F )de l'echelle de Mulliken.
Le rayon atomique est par contre evalue tres correctement par la formule donnee (voir exercice suivant). L’electronegativite d’Alred et Rochow basee sur la valeur de R est en consequence tres correctement evaluee elle aussi.
Exercice 3
Z* |
n |
n2/Z* |
R Calcule |
R experimental |
|
F |
5,2 |
2 |
0,77 |
0,69 |
0,72 |
O |
4,55 |
2 |
0,88 |
0,71 |
0,73 |
S |
5,45 |
3 |
1,65 |
1,02 |
1,02 |
Be |
1,95 |
2 |
2,05 |
0,96 |
0,90 |
Si |
4,15 |
3 |
2,17 |
1,13 |
1,11 |
Mg |
2,85 |
3 |
3,16 |
1,35 |
1,36 |
Classements
On constate que la valeur de n2/Z* permet un classement qualitatif des atomes, malgre une inversion (S et Be).
La formule R = 0,215 n2/Z* + 0,148 n + 0,225 permet un calcul assez precis des valeurs des rayons de covalence et un bon accord avec les valeurs experimentales. (voir article BUP)
Exercice 4 :
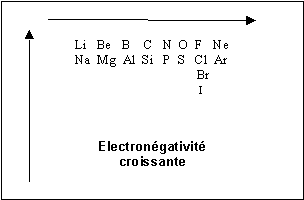
Li < N < O ( meme ligne)
Si < P < Cl ( meme ligne )
I < Br < Cl < F ( meme colonne )
Pour comparer deux elements qui ne sont ni dans la meme ligne ni dans la meme colonne, on calculera par exemple l’electronegativite de Alred et Rochow facilement accessible.
Exercice 5 :
Affectons l’anion de l’indice A et le cation de l’indice C.
d = RC + RA
RC = k nC2 / Z*C
RA = k nA2 / Z*A
RC / RA = ( nC2 / nA 2 ) ( Z*A / Z*C )
RC = ( nC2 / nA 2 ) * ( Z*A / Z*C ) * RA = K RA
D = ( K + 1 ) RA
RA = d / ( K + 1 )
RC = K RA
| d | Z*C | nC | Z*A | nA | K | RA | RC | |
| NaF | 2,31 | 6,85 | 2 | 4,85 | 2 | 0,708 | 1,35 | 0,96 |
| LiF | 2,01 | 2,7 | 1 | 4,85 | 2 | 0,449 | 1,39 | 0,62 |
Les valeurs trouvees pour le rayon ionique du fluor ne sont pas tout a fait identiques mais sont tout de meme tres proches.
Cette methode tres simple permet donc d’evaluer de proche en proche les valeurs des differents rayons ioniques. Une valeur moyenne sera retenue a partir de determinations sur plusieurs solides ioniques differents. Ces valeurs des rayons ioniques de Pauling ont ete tabulees et sont largement utilisees en cristallographie.
D’autres tables plus modernes existent, telle que la table de Schanon et Prewitt qui ont correles les distances inter-nucleaires de plus de mille oxydes. En pratiques les differences sont faibles entre les diverses tables et la table de Pauling est encore tres utilisee actuellement.
Exercice 6 :
Pour attribuer a chaque element sa colonne, il suffit de chercher pour quelle ionisation on observe une brusque elevation. Ce saut correspond a la structure du gaz rare tres stable.
Element X : le saut se produit pour la quatrieme ionisation. X3+ possede la structure d’un gaz rare et X appartient a la colonne 13 de la classification : X = B ou Al.
Elements Y et Z : le saut se produit pour la cinquieme ionisation. X4+ et Z4+ possedent la structure d’un gaz rare et X et Z appartiennent a la colonne 14 de la classification : Y et Z = C ou Si.
Element W : le saut se produit pour la deuxieme ionisation. X+ possede la structure d’un gaz rare et X appartient a la colonne 1 de la classification : W = Li ou Na.
Parmi les elements possibles (B, Al, C, Si, Li et Na) on peut eliminer Li puisque celui-ci ne possede que trois electrons et ne peut donc avoir 5 ionisations successives. L’element W est donc le sodium Na.
Les atomes Y et Z appartiennent a la meme colonne. Cela se traduit par une grande similitude des courbes (parallelisme evident).
L’energie de premiere ionisation varie en sens inverse du rayon atomique.
Plus l’atome est petit, plus l’electron est pres du noyau et plus il est difficile a arracher.
Le rayon atomique variant sensiblement comme n2/Z* augmente quand on descend dans une colonne car l’augmentation de n2 l’emporte largement sur celle de Z*. L’element ayant l’energie de premiere ionisation la plus elevee est donc l’element situe le plus haut.
Y est le carbone et Z le silicium.
Il ne reste qu’a identifier X qui peut etre B ou Al.
Calculons les trois premieres energies d’ionisation de B :
| B | 1s2 | 2s2 , 2 p1 |
| 2 E1 | 3 E2 | |
| B+ | 1s2 | 2s2 |
| 2 E1 | 2 E'2 | |
| B2+ | 1s2 | 2s1 |
| 2 E1 | E''2 | |
| B3+ | 1s2 | |
| E1 |
EB = 2 E1 + 3 E2 EB+ = 2 E1 + 2 E’2 EB2+ = 2 E1 + E’’2 EB3+ = 2 E1
Energie de premiere ionisation : B à B+ + 1 e- E.I.1 = EB+ - EB = 2 E’2 – 3 E2
Energie de deuxieme ionisation : B+ à B2+ + 1 e- E.I.2 = EB2+ - EB+ = E’’2 – 2 E’2
Energie de troisieme ionisation : B2+ à B3+ + 1 e- E.I.3 = EB3+ - EB2+ = - E’’2
E2 = -13,6 * Z*E22 / 4 E’2 = -13,6 * Z*E’22 / 4 E’’2 = -13,6 * Z*E’’22 / 4
Z*E2 = Z*B = 5 – ( 2 * 0,35 ) – ( 2 * 0,85 ) = 2,6
Z*E’2 = Z*B+ = 2,6 + 0,35 = 2,95
Z*E’’2 = Z*B2+ = 2,95 + 0,35 = 3,3
E2 = -13,6 * 2,62 / 4 = -22,98 eV
E’2 = -13,6 * 2,952 / 4 = -29,58 eV
E’’2 = -13,6 * 3,32 / 4 = -37,03 eV
E.I.1 = 2 E’2 – 3 E2 = ( 2 * -29,58 ) – ( 3 * - 22,98 ) = 9,8 eV
E.I.2 = E’’2 – 2 E’2 = -37,03 – ( 2 * -29,58 ) = 22,1eV
E.I.3 = - E’’2 = 37,0 eV
Calcule pour B |
Experimental pour X |
Ecart % |
|
E.I.1 |
9,8 |
8,26 |
18,6 |
E.I.2 |
22,1 |
25 |
-11,6 |
E.I.3 |
37,0 |
37,8 |
-2,1 |
L’examen du tableau montre que les valeurs calculees pour le Bore s’accordent assez bien avec celles donnees pour l’atome X. On peut donc supposer que X est le Bore.
| Al | 1s2 | 2s2 , 2p6 | 2s2 , 2 p1 |
| 2 E1 | 8 E2 | 3 E3 | |
| Al+ | 1s2 | 2s2 , 2p6 | 2s2 |
| 2 E1 | 8 E2 | 2 E'3 | |
| Al2+ | 1s2 | 2s2 , 2p6 | 2s1 |
| 2 E1 | 8 E2 | E''3 | |
| Al3+ | 1s2 | 2s2 , 2p6 | |
| E1 | 8 E2 |
Al 1s2 2s2, 2p6 3s2 , 3p1 ( E1, E2 ,E3 )
Al+ 1s2 , 2s2 2p6 , 3s2 ( E1 , E2 , E’3 )
Al2+ 1s2 , 2s2 2p6 , 3s1 ( E1 , E2 , E’’3 )
Al3+ 1s2 2s2, 2p6 ( E1 , E2)
EAl = 2 E1 + 8 E2 + 3 E3
EAl+ = 2 E1 + 8 E2 + 2 E’3
EAl2+ = 2 E1 + 8 E2 + E’’3
EAl3+ = 2 E1 + 8 E2
Energie de premiere ionisation : Al à Al+ + 1 e- E.I.1 = EAl+ - EAl = 2 E’3 – 3 E3
Energie de deuxieme ionisation : Al+ à Al2+ + 1 e- E.I.2 = EAl2+ - EAl+ = E’’3 – 2 E’3
Energie de troisieme ionisation : Al2+ à Al3+ + 1 e- E.I.3 = EAl3+ - EAl2+ = - E’’3
E3 = -13,6 * Z*E32 / 4 E’3 = -13,6 * Z*E’32 / 4 E’’3 = -13,6 * Z*E’’32 / 4
Z*E3 = Z*Al = 13 – ( 2 * 0,35 ) – ( 8 * 0,85 ) – ( 2 * 1 ) = 3,5
Z*E’3 = Z*Al+ = 3,5 + 0,35 = 3,85
Z*E’’3 = Z*Al2+ = 3,85 + 0,35 = 4.2
E3 = -13,6 * 3,52 / 9 = -18,51 eV
E’3 = -13,6 * 3,852 / 9 = -22,40 eV
E’’3 = -13,6 * 4,22 / 9 = -26,66 eV
E.I.1 = 2 E’3 – 3 E3 = ( 2 * -22,40 ) – ( 3 * - 18,51 ) = 10,7 eV
E.I.2 = E’’3 – 2 E’3 = -26,66 – ( 2 * -22,40 ) = 18,1 eV
E.I.3 = - E’’3 = 26,7 eV
Experimental pour X |
Calcule pour Al |
Experimental pour Al | Ecart % |
|
E.I.1 |
8,26 |
10,7 |
6,0 |
78 |
E.I.2 |
25 |
18,1 |
18,8 |
-3,7 |
E.I.3 |
37,8 |
26,7 |
28,5 |
-6,3 |
L’examen du tableau montre que les valeurs calculees pour l’Aluminium ne s’accordent aucunement avec les donnees concernant l’atome X. L’atome X n’est donc pas l’Aluminium mais bien le Bore comme nous l’avions trouve precedemment.
En revanche les valeurs calculees pour E.I2 et E.I3 s’accordent assez bien avec les valeurs experimentales (colonne 4), ce qui confirme l’interet des regles de Slater. L’ecart enorme trouve pour E.I1 peut s’expliquer par les configurations electroniques de Al et Al+.
Al+ possedant une couche completement remplie est stabilise, il est donc forme facilement et E.I 1 est "anormalement " faible. (voir exercice 1)
![]()