D_RH⁰₅ = D_RH⁰₁ + 3 D_RH⁰₂ - D_RH⁰₃ + 3 D_RH⁰₄

D_RH⁰₅ = -3272,94 + 3*-242,02 + 3925,02 + 3*-43,47 = -204,39 KJ.mol^-1

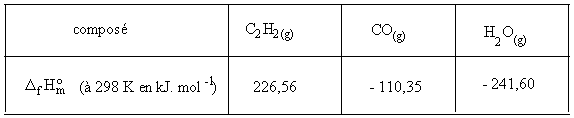
D_RH⁰ = S n_i D_RH_f⁰_i

D_RH⁰ = 2*-110,35 + -241,60 - 226,56 - 3/2 * 0 = -668,86 KJ.mol^-1

Calculer l'enthalpie de la réaction suivante à 298 K, DrH°.

C₂H₆ (g) + 7/2 O₂ (g) = 2 CO₂ (g) + 3 H₂O (g)

On donne :

D_RH⁰ = S E liaison détruites - S E liaisons formées

D_RH⁰ = 347,36 + 6*410,48 + 7/2*493,24 - 4*798,38 - 6*462,31 = -1430,8 KJ.mol^-1

2°) Calculer D_RH°₃₉₈

On donne :

C°p,m(C₂H₆,g) = 53,1 J mol.-1 K-1

C°p,m(O₂,g) = 29,47 J mol.-1 K-1

C°p,m(CO₂,g) = 37,24 J mol.-1 K-1

C°p,m(H₂O,g) = 32,14 J mol.-1 K-1

On supposera C°p,m constant dans l'intervalle de température considérée.

D_RH⁰_T = D_RH⁰_{T0 +} · DCp⁰ _dT

D_RG⁰ = S n_i D_RG_f⁰_i

D_RG⁰ = 2*- 370,37 - 2*-300,37 - 0 = -140 KJ.mol^-1

D_RG⁰ = -R T ln K è K = exp(-D_RG⁰/RT) = 3,47 10²⁴

1) Déterminer D_RG⁰₃₀₀

2) Déterminer DRH⁰ et D_RS⁰ en supposant qu'elles sont indépendantes de la température.

1) D_RG⁰ = - R T ln K = -8,314*300*ln35608 = -26140 J.mol^-1

2) D_RG⁰ = D_RH⁰ - TD_RS⁰ = - R T ln K

- D_RH⁰ / R T + D_RS⁰ / R = ln K

Si on porte ln K = f (1 / T) on obtient une droite de pente P = - D_RH⁰ / R et d'ordonnée à l'origine O = D_RS⁰ / R

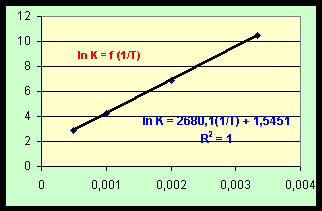
 P = - D_RH⁰ / R è D_RH⁰ = - P * R

 P = 2680,1 è D_RH⁰ = -22281,5 J.mol^-1

O = D_RS⁰ / R è D_RS⁰ = O * R

O = 1,541 è D_RS⁰ = 12,8 J.mol^-1K^-1

 Exercice 6

1) Prévoir sans calculs et en justifiant simplement votre réponse :

a) le signe de D_RH⁰

On voit que K augmente quand T augmente

Principe de Le Chatelier : Réaction endothermique et donc D_RH⁰ > 0

Loi de Vant'hoff : d ln K / dT = D_RH⁰ / RT²

d ln K et dT ont même signe puisqu'il varient dans le même sens. { d ln K / dT } > 0

RT² est positif donc D_RH⁰ > 0 et réaction endothermique.

b) le signe de D_RS⁰

A(g) + B(s) = 2 C(g)

L'augmentation du nombre de mole gazeuse fait augmenter le désordre et donc D_RS⁰ > 0.

2) Déterminer les valeurs de D_RH⁰ et D_RS⁰

On pourrait comme précédemment faire une résolution graphique.

On peut plus rapidement se contenter d'utiliser deux points seulement.

 P = Dy / Dx = (-4,0174 - 1,0025) / (0,003333 - 0,001666) = -3011

O = y - Px = -4,0174 + 3011 * 0,00333 = 6,009

Soit D_RH⁰ = - P * R = 3011 * 8,314 = 25036 J.mol^-1

Et D_RS⁰ = O * R = 6,009 * 8,314 = 49,96 J.mol^-1.K^-1

 3) On appelle température d'inversion d'un équilibre la température pour laquelle sa constante est égale à l'unité. Déterminer la température d'inversion de cet équilibre.

D_RG⁰ = D_RH⁰ - TD_RS⁰ = - R T ln K = - R T ln 1 = 0

D_RH⁰ = T D_RS⁰

T = D_RH⁰ / D_RS⁰ = 25036 / 49,96 = 501 K (soit 228 °C)

4) Prévoir qualitativement l'influence d'une augmentation de pression sur cet équilibre.

A(g) + B(s) = 2 C(g)

Le nombre de mole gazeuse augmente au cours de la réaction.

Principe de Le Chatelier : L'équilibre s'oppose à l'augmentation de pression en se déplaçant dans le sens de diminution du nombre de mole gazeuses = Sens 2 = dissociation de C en A et B

5) Prévoir qualitativement l'influence à pression constante :

• a) de l'ajout d'une petite quantité de A

DG = DG⁰ + RT ln Q = -RT ln K + RT ln Q = RT ln (Q / K )

K ne dépend que de T, il suffit de regarder comment Q varie pour prévoir dans quel sens l'équilibre se déplace.

On suppose que T est maintenue constante.

A(g) + B(s) = 2 C(g)

Q = a_C² / { a_A a_B }

a_C = P_C a_A = P_A aC = x_C = 1

Q = P_C² / P_A = [ n_C² P²/ nt² ] * [ nt / nA P ] = n_C² P / ( n_A nt )

L'ajout de A fait augmenter n_A et nt ce qui fait diminuer Q et donc DG, si on suppose que l'on était à l'équilibre DG devient négatif et l'équilibre se déplace donc dans le sens 1 de formation de C.

• b) de l'ajout d'une petite quantité de B

Q = n_C² P / ( n_A nt )

attention : nt est le nombre total de mole gazeuses

B est un solide, Q ne dépend pas de n_B il n'y donc aucun effet sur l'équilibre.

• c) de l'ajout d'une petite quantité de C

Q = n_C² P / ( n_A nt ) (avec P et n_A constants)

Q = n_C² / n_A * P /nt = cte * n_C² / n_A

Q va augmenter car le terme n_C² du numérateur augmente plus rapidement que le terme nt (= nA + nC) du dénominateur. La fonction représentant Q est une parabole croissante car nA et nC qui sont des nombre de moles sont forcément positifs. DG va donc augmenter, si on suppose qu'on était à l'équilibre au moment de l'ajout du C supplémentaire on voit que DG devient positif. L'équilibre se déplace donc dans le sens 2.

 Exercice 7 :

On donne E⁰ Fe³⁺/Fe²⁺ = 0,77 V et E⁰ Fe²⁺/Fe = -0,44 V. Calculer E⁰ Fe³⁺/Fe

DG⁰₃ = DG⁰₁ + DG⁰₂

E⁰₃ = ( E⁰₁ + 2 E⁰₂ ) / 3 = (0,77 + 2 * -0,44 ) / 3 = -0,037 V

 Exercice 8 :

On étudie l’équilibre d’estérification entre l’acide éthanoïque (CH₃COOH) et le méthanol (CH₃OH) qui fournit de l’éthanoate de méthyle (CH₃COOCH₃) et de l’eau.

- Ecrire l’équilibre correspondant.

- Lors d’une expérience, on mélange 6 g d’acide éthanoïque pur et 3,2 g de méthanol pur. On laisse la réaction se faire jusqu’a ce que l’équilibre soit établi. On analyse alors le mélange réactionnel et on trouve qu’il s’est formé 0,07 mole d’eau. Calculer la constante de cet équilibre.

- Lors d’une autre expérience on fait réagir 10 g d’acide éthanoïque pur et 20g de méthanol pur. Quelle sera la composition du mélange à l’équilibre ?

• Lors d’une troisième expérience on mélange 1 mole d’éthanoate de méthyle et 36 g d’eau. Quelle sera la composition du mélange à l’équilibre ?

 Ecrire l’équilibre correspondant.

CH₃COOH (l) + CH₃OH(l) = CH₃COOCH₃ (l) + H₂O(l)

* Lors d’une expérience, on mélange 6 g d’acide éthanoïque pur et 3,2 g de méthanol pur. On laisse la réaction se faire jusqu’a ce que l’équilibre soit établi. On analyse alors le mélange réactionnel et on trouve qu’il s’est formé 0,07 mole d’eau. Calculer la constante de cet équilibre.

nCH₃COOH = 6 / ( 24+4+32) = 6 / 60 = 0,1 mole

nH₂O = n CH₃COOCH₃ = x = 0,07 mole

nCH₃COOH = 10 / ( 24+4+32) = 10 / 60 = 0,167 mole

5,444 = x²/((0,167-x)(0,625-x))

5,444 (0,167-x) (0,625-x) = x²

5,444 x² - 4,312 x + 0,5682 = x²

4,444 x² - 4,312 x + 0,5682 = 0

D = 4,312² - 4*4,444*0,5682 = 8,493

Ö D = 2,914

x1 = (4,312 + 2,914) / (2*4,444) = 0,813 mole

x2 = (4,312 - 2,914) / (2*4,444) = 0,157 mole

Or x est obligatoirement inférieur à 0,167 mole on ne garde donc que la solution physiquement possible : x = 0,1573

n CH₃COOH = 0,0097 mole

n CH₃OH = 0.4677 mole

n CH₃COOCH₃ = n H₂O = 0,1573 mole

 On peut vérifier que le nombre de mole total est bien égal à sa valeur initiale

0,1573 + 0,1573 + 0.0097 + 0,4677 = 0,792 = 0,167 + 0,625

- Lors d’une troisième expérience on mélange 1 mole d’éthanoate de méthyle et 36 g d’eau. Quelle sera la composition du mélange à l’équilibre ?

5,444 = (1 + x) (2 + x)) / x²

5,444 x² = (1 + x) (2 + x)

5,444 x² = x² + 3x + 2

4,444 x² - 3 x - 2 = 0

D = 3² + 4*4,444*2 = 44,55

Ö D = 6,675

x1 = (3 + 6,675) / (2*4,444) = 1,089 mole

x2 = (4,312 - 2,914) / (2*4,444) = -0,413 mole

Or x est obligatoirement négatif et on ne garde donc que x = -0,413

n CH₃COOH = 0,413 mole

n CH₃OH = 0,413 mole

n CH₃COOCH₃ = 0,5865 mole

n H₂O = 1,5865 mole

On peut vérifier que le nombre de mole total est bien égal à sa valeur initiale

0,413 + 0,413 + 0,5865 + 1,5865 = 2,999 = 1 + 2

D_RG⁰₅ = D_RG⁰₁ + D_RG⁰₂ - D_RG⁰₄

2 D_RG⁰₆ = 2 D_RG⁰₂ - D_RG⁰₄ + D_RG⁰₃

D_RG⁰₇ = D_RG⁰₁ - D_RG⁰₅ + D_RG⁰₆